Speaker
Description
A natural way to control turbulence in magnetic fusion devices is to take advantage of zonal flows, which form spontaneously and can reduce the turbulence level. Zonal flows can even suppress turbulence completely in a certain parameter range where drift-wave instabilities would otherwise develop. But exploiting this effect, known as the Dimits shift, requires understanding of its physics, which has been unclear. Here, a generic understanding of the Dimits shift in electrostatic drift-wave turbulence is obtained, for the first time, by studying the tertiary instability of a zonal flow within reduced turbulence models (Ref. 1). We show that tertiary modes are localized near extrema of the zonal-flow velocity $U(x)$ with respect to the radial coordinate $x$. These modes can be described as quantum harmonic oscillators with complex frequencies, so their spectrum can be readily calculated. The corresponding growth rate $\gamma_{\rm TI}$ is derived within the modified Hasegawa--Wakatani model. We show that $\gamma_{\rm TI}$ equals the primary-instability growth rate plus a term that depends on the local flow "curvature" ${\rm d}^2U/{\rm d}x^2$; hence, the instability threshold is shifted compared to that in homogeneous turbulence. This shift is the Dimits shift, which we find explicitly in the Terry--Horton limit, and our analytic predictions agree well with results of numerical simulations. Our theory of the tertiary instability also extends to other turbulence models. For example, the key features of the tertiary instability of ion-temperature-gradient mode are reproduced by our theory and verified by gyrokinetic simulations.
Plasma microturbulence causes anomalous transport of particles and energy and sets the core plasma profile in tokamaks, where the underlying "primary" drift-wave (DW) instabilities develop if the plasma temperature and (or) density gradient exceed a certain threshold. However, having their linear growth rate $\gamma_{\rm PI}$ above zero is not enough to make plasma turbulent, because the "secondary instability" can suppress turbulence by generating zonal flows (ZFs); hence, the threshold for the onset of turbulence is modified compared to the linear theory. This constitutes the so-called Dimits shift (Ref. 2), which has been attracting attention for two decades. The finite value of the Dimits shift is commonly attributed to the "tertiary instability" (TI) (Ref. 3), and some theories of the TI have been proposed. However, basic understanding and generic description of the TI and the Dimits shift have been elusive.
Here, we propose a quantitative theory of the TI based on reduced models of DW turbulence; we also use this theory to explain the Dimits shift and, in some cases, even to calculate it semi-analytically (Ref. 1). We start by noticing that according to several numerical studies (Refs. 3-5), DW turbulence in the Dimits regime is localized near extrema of the ZF velocity $U(x)$. Assuming such localization, we derive an approximate equation that governs the localized DW modes. This equation coincides with that of a quantum harmonic oscillator with a complex frequency; hence, the mode structures and the growth rates are readily found analytically. Having $\gamma_{\rm TI} = 0$ corresponds to the threshold at which plasma becomes turbulent. This threshold is shifted relative to that of the primary instability in homogeneous turbulence, and that is precisely the Dimits shift.
Using the modified Hasegawa--Wakatani model, we calculate $\gamma_{\rm TI}$ analytically (Fig. 1) and find that the TI has features different from those that are commonly expected. First, the TI modes are different near maxima and minima of the ZF velocity and has a broad Fourier spectrum (in $x$); hence, they cannot be described adequately within the few-harmonic approximation, contrary to some previous theories. Second, the growth rates can be written as $\gamma_{\rm TI}=\gamma_{\rm PI}+\Delta\gamma(\mathcal{C})$, where $\mathcal{C}\doteq {\rm d}^2U/{\rm d}x^2$ is the local ZF "curvature", and $\Delta\gamma$ becomes zero in the absence of the ZF. Therefore, the TI can be considered as a primary instability modified by the ZF curvature. The fact that $\Delta\gamma$ is controlled by the ZF curvature is in variance with the conventional understanding that turbulence is regulated by the ZF shear $|{\rm d}U/{\rm d}x|$. Also contrary to what is commonly assumed, the TI is distinct from the Kelvin--Helmholtz instability. In the modified Hasegawa--Wakatani model that we use, Kelvin--Helmholtz modes are stabilized by the adiabatic electron response, while the TI is still present. Similar features of the TI are found within the ion-temperature-gradient-mode model introduced in Ref. 3. This has been tested in slab-geometry gyrokinetic simulations using the code $\mathsf{GS2}$ (Ref. 7).

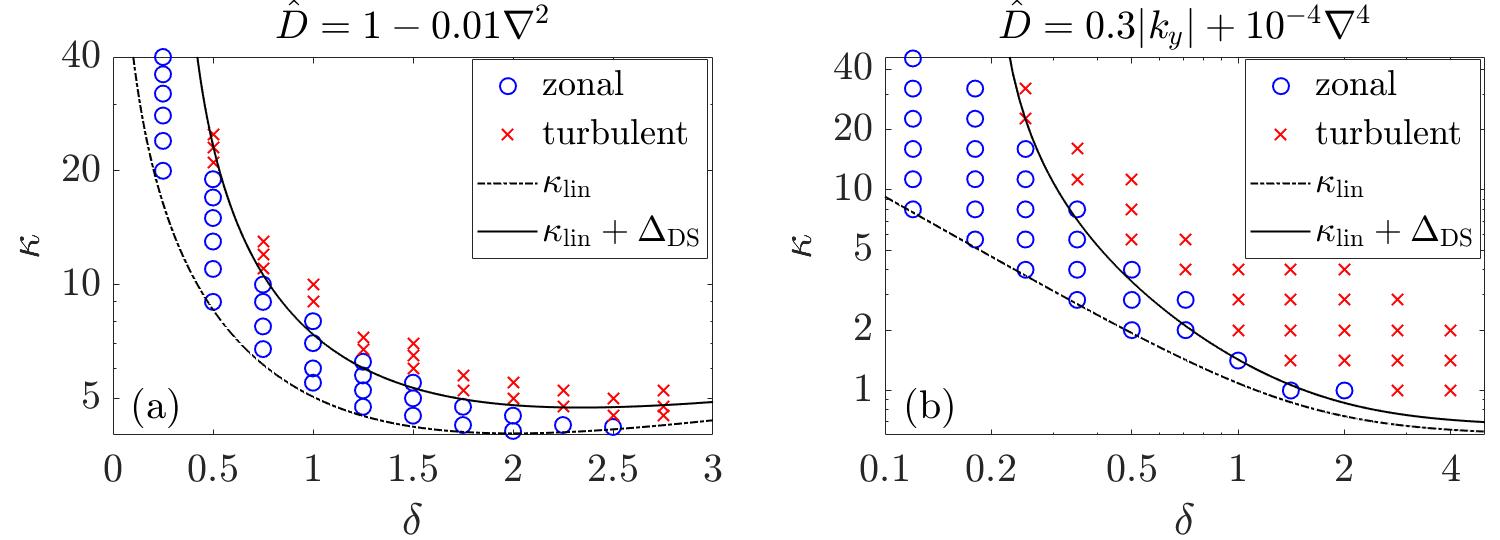
Understanding the growth rate $\gamma_{\rm TI}=\gamma_{\rm PI}+\Delta\gamma(\mathcal{C})$ provides a generic explanation of the Dimits shift. We have calculated $\Delta \gamma(\mathcal{C})$ explicitly within the modified Terry--Horton model (as the adiabatic limit of the Hasegawa--Wakatani model) and used those results to determine the Dimits shift in this model. As seen in Fig. 2, our theory shows good agreement with simulations.
In summary, our work provides a generic qualitative understanding of the Dimits shift and also leads to (semi-) analytic predictions of this shift within a number of reduced models of DW turbulence.
This work was supported by the US DOE through Contract No. DE-AC02-09CH11466. This work made use of computational support by CoSeC, the Computational Science Centre for Research Communities, through CCP Plasma (EP/M022463/1) and HEC Plasma (EP/R029148/1).
(1) H. Zhu, Y. Zhou, and I. Y. Dodin, Phys. Rev. Lett. 124, 055002 (2020).
(2) A. M. Dimits et al., Phys. Plasmas 7, 969 (2000).
(3) B. N. Rogers, W. Dorland, and M. Kotschenreuther, Phys. Rev. Lett. 85, 5336 (2000).
(4) S. Kobayashi and B. N. Rogers, Phys. Plasmas 19, 012315 (2012).
(5) R. Numata, R. Ball, and R. L. Dewar, Phys. Plasmas 14, 102312 (2007).
(6) D. A. St-Onge, J. Plasma Phys. 83, 905830504 (2017).
(7) M. Barnes et al., GS2 v8.0.2, https://doi.org/10.5281/zenodo.2645150.
| Affiliation | Princeton Plasma Physics Laboratory |
|---|---|
| Country or International Organization | United States |
