Speaker
Description
Tearing modes with poloidal/toroidal mode numbers $m$/$n$ = 2/1 have been routinely observed in KSTAR [1] with modes having notably large amplitude leading to significantly reduced both normalized beta, $\beta_N$, and plasma stored energy. Global kink/ballooning or resistive wall modes (RWMs) are observed to be stable at high $\beta_N$ above the $n$ = 1 ideal MHD no-wall stability limit, $\beta_N^{no-wall}$. Global MHD stability modified by kinetic effects can explain the observed RWM stable plasma operation above $\beta_N^{no-wall}$ through stabilization by kinetic effects [2]. The observed 2/1 modes onset at relatively low $\beta_N$ ~ 1.4 in the early phase of the discharge with electron cyclotron heating (ECH) applied to the core region of the plasma. Neighboring MHD activity that could trigger the mode by providing a seed island is not observed. The destabilized 2/1 mode initially has a small amplitude and growth rate, and by considering its ‘triggerless’ nature, the mode at low $\beta_N$ could be driven by an island resulting from a current density profile yielding instability to the 2/1 mode which can be represented by a positive tearing stability index, $\Delta'$, at the $q$ = 2 surface. In contrast, a comparable 2/1 mode which onsets at high $\beta_N$ ~ 3.5 above $\beta_N^{no-wall}$ coincides with large ELM crashes observed that can trigger the mode, and has significantly faster mode growth. Although their onset conditions and mechanisms appear to be different, once these islands grow above the critical island size of the neoclassical tearing mode (NTM), they commonly could grow dominantly by neoclassical pressure-driven effects. The resistive MHD stability examined by the resistive DCON code [3] is compared between these 2/1 modes destabilized at different $\beta_N$ and onset conditions. The $\Delta'$ from resistive DCON indicates that once the 2/1 mode onsets and saturates, the computed $\Delta'$ is commonly unstable ($\Delta'$ > 0). A stable $\Delta'$ is computed in the high $\beta_N$ > $\beta_N^{no-wall}$ phase where the ‘triggered’ 2/1 mode onset is observed indicating that the stability is apparently consistent with a linearly stable NTM.
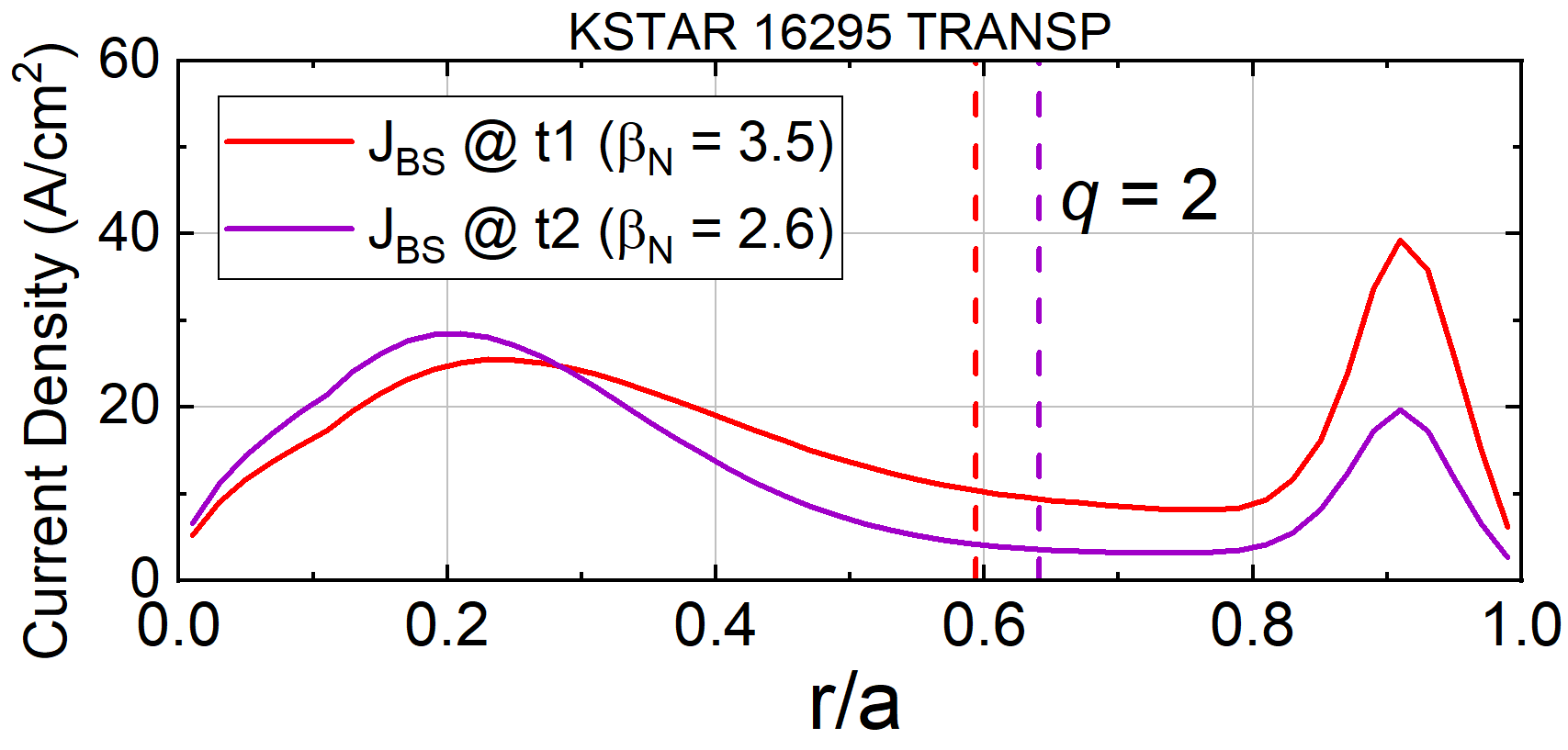
The NTM island growth rate is described by the modified Rutherford equation (MRE) [4], $\tau_R$ $\partial w$/$\partial t$ = $\Delta'$($w$) + $k_{NC}$$\Delta'_{NC}$ − $k_{pol}$$\Delta'_{pol}$ − $\Delta'_{GGJ}$ − $\Delta'_{CD}$. To identify the governing destabilization mechanism in the mode stability, the neoclassical drive term $\Delta'_{NC}$ in MRE which is given by $\Delta'_{NC}$($w$) = 16$J_{BS}$$/$($sw \langle J \rangle$) is computed by the TRANSP code. The magnitude of the $\Delta'_{NC}$ is computed to be large with values in the range 2.4–2.8 for the equilibria at high $\beta_N$ in which the NTM stability is expected to be unstable suggesting the dominant effect of the pressure-driven bootstrap current in the mode destabilization. The $\Delta'_{NC}$ becomes significantly lower in the range 0.6-0.9 after the island saturates and the confinement is consequently degraded. The TRANSP computed bootstrap current ($J_{BS}$) profiles for the ‘triggered’ 2/1 mode in the high $\beta_N$ discharge are shown in FIG. 1. In the fairly broad $J_{BS}$, the distinctive edge $J_{BS}$ is created by the steep edge pressure pedestal. The $J_{BS}$ at the $q$ = 2 surface is reduced almost by a factor of 3 after the mode saturation. The total non-inductive current fraction reached 64% in the high $\beta_N$ equilibrium before the mode onset. The remaining terms in the MRE are computed to develop a preliminary NTM stability model for the high $\beta_N$ KSTAR plasma. In the MRE, the critical island width, $w_d$, which accounts for the transport threshold due to small island size is calculated by assuming somewhat reduced transport anisotropy, $\chi_\perp$$/$$\chi_\parallel$, in the range 1e$^{-11}$-1e$^{-9}$ inside the island. The $w_d$ is computed to be ~1 cm for the anisotropy values examined.
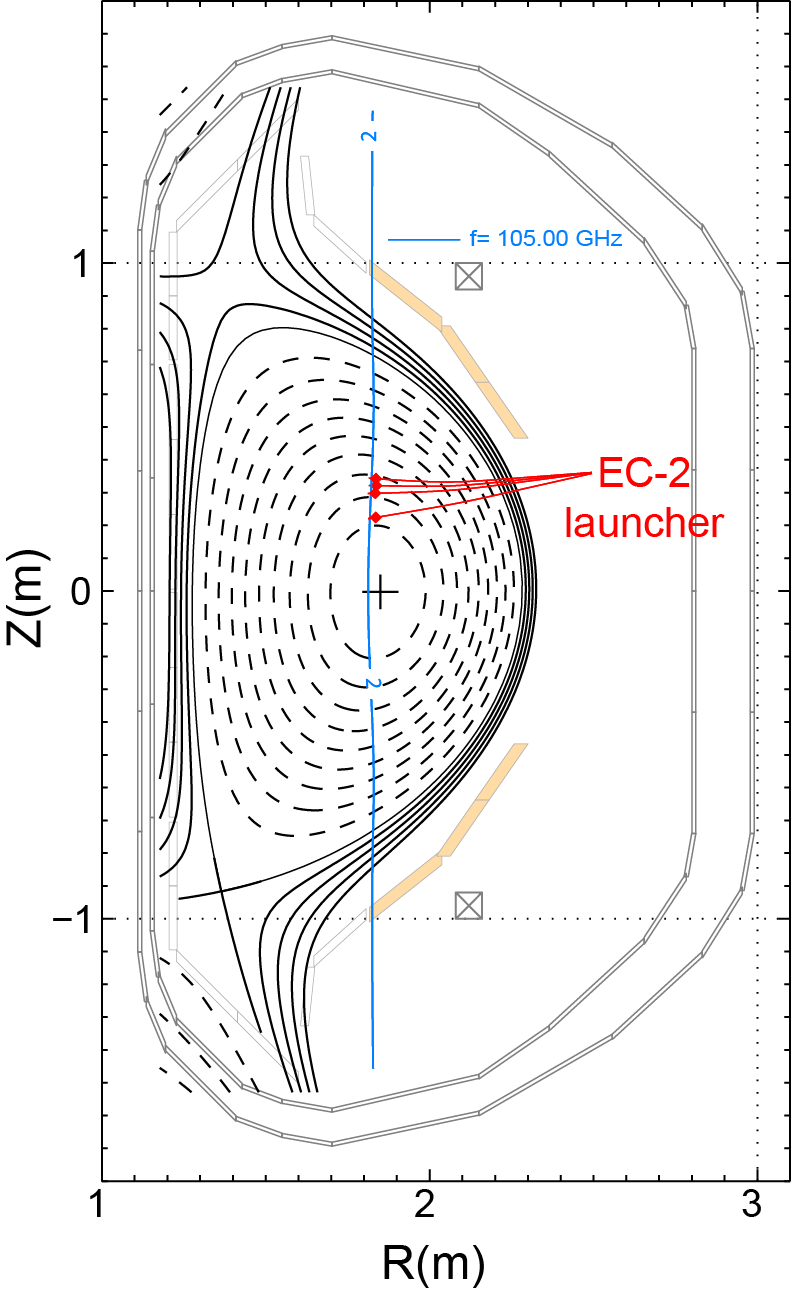
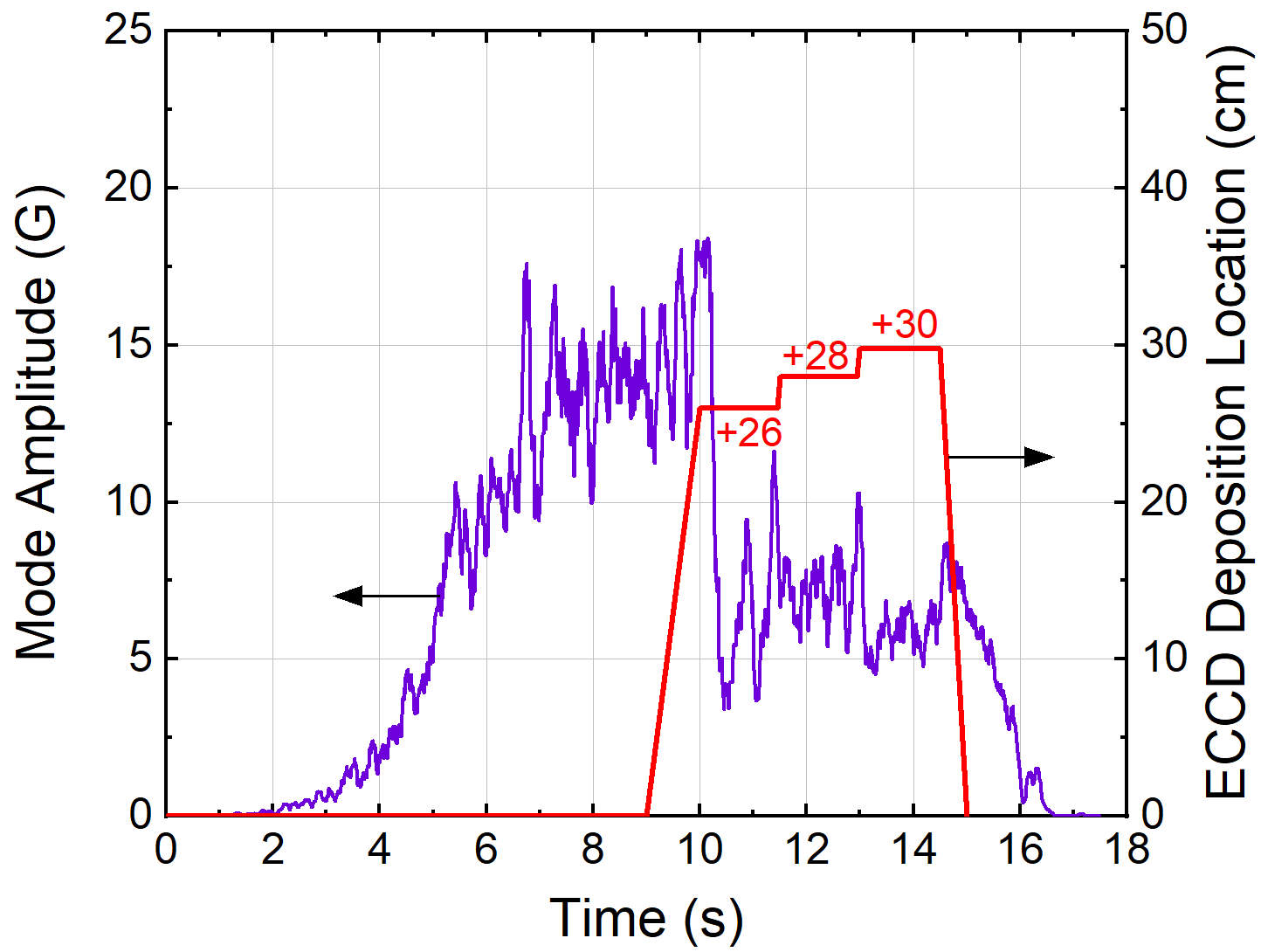
For high beta plasma operation, active stabilization of NTMs by compensating the perturbed $J_{BS}$ by utilizing the electron cyclotron current drive (ECCD) has been studied on KSTAR. The EC wave can be launched from the two real-time steerable launchers located at above and below the midplane. The EC system can produce a wave frequency of 105 or 140 GHz, and under the operating toroidal field in the range 1.8-2.0 T used in typical H-mode discharges, the 105 GHz, second harmonic ECCD is used to drive localized current in the island. Figure 2 shows the ray trajectories of the 105 GHz ECCD launched from the upper midplane launcher (EC-2) in the experiment which drive current on the resonance intersection at Z = +20, +26, +28 and +30 cm along the second harmonic resonance layer with $B_T$ = 1.9 T computed by the TORAY-GA ray-tracing code. The trajectory to the resonance intersection on the same Z > 0 along the resonance layer is used since it can generate a relatively narrow current profile width ($\delta_{EC}$) with a higher current density ($J_{EC}$) beneficial for NTM stabilization. The EC deposition location is varied in steps around the estimated $q$ = 2 surface location using the 2D ECE imaging diagnostic in the experiment. By using a total EC power of 0.75 MW, a localized $J_{EC}$ having a peak magnitude of ~7 A/cm$^2$ on the mode rational surface is computed when the 2/1 mode amplitude is decreased by ~80% due to the ECCD suitably aligned on the island shown in FIG. 3. The computed peak $J_{EC}$ magnitude somewhat smaller than the $J_{BS}$ of ~10 A/cm$^2$ at $q$ = 2 (FIG. 1) could be responsible for the partial stabilization of the mode amplitude. The results indicate that active stabilization of the 2/1 NTM by ECCD is plausible by using a total available EC power of 1.5 MW from the two EC systems on KSTAR. To analyze the NTM stabilization by the effect of ECCD ($\Delta'_{CD}$), the MRE model is examined by fitting the model by using the experimental data. The electron profiles and equilibrium conditions maximizing the control performance are investigated. This study will provide the required foundation for active stabilization of NTMs which is a critical need for high beta plasma operation in KSTAR.
Supported by US DOE Grant DE-SC0016614
[1] Y.S. Park, S.A. Sabbagh, W.H. Ko, et al., Phys. Plasmas 24 (2017) 012512
[2] J.W. Berkery, S.A. Sabbagh, R. Betti, et al., Phys. Rev. Lett. 104 (2010) 035003
[3] A.H. Glasser, Z.R. Wang and J.K. Park, Phys. Plasmas 23 (2016) 112506
[4] E.D. Fredrickson, M. Bell, R.V. Budny, et al., Phys. Plasmas 7* (2000) 4112
| Affiliation | Columbia University |
|---|---|
| Country or International Organization | United States |
