Speaker
Description
New studies identify the critical parameters and physics governing disruptive neoclassical tearing mode (NTM) onset. A m/n=2/1 mode in DIII-D begins to grow robustly only after a seeding event (ELM Fig. 1, or sawtooth precursor and crash Fig. 2) causes the mode rotation to drop close to that of the plasma’s Er=0 rest frame; this condition opens the stabilizing ion-polarization current “gate” and destabilizes an otherwise marginally stable NTM. Our new experimental and theoretical insights and novel toroidal theory-based modeling are benchmarked and scalable to ITER and other future experiments. The nominal ITER rotation at q=2 is found to be stabilizing (“gate closed”) except for MHD-induced transients that could “open the gate.” Extrapolating from the DIII-D ITER baseline scenario (IBS) discharges, MHD transients are much more likely to destabilize problematic 2/1 NTMs in ITER; this makes predictions of seeding and control of both ELMs and sawteeth imperative for more than just “simply” minimizing divertor pulsed-heat loading.
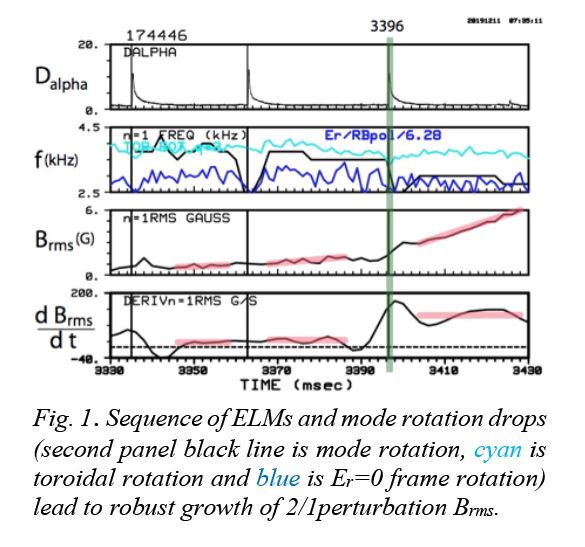
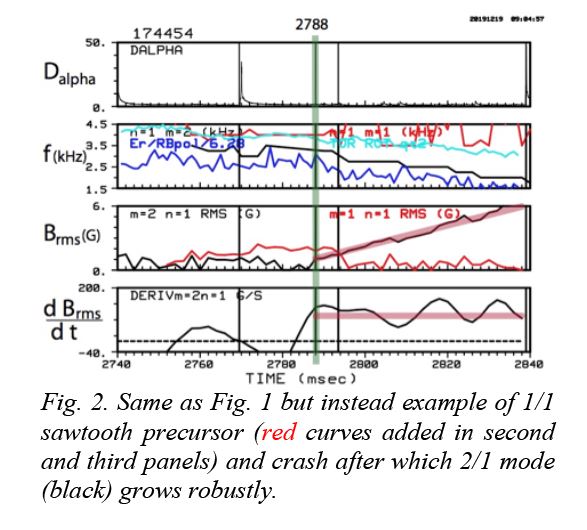
While nearly steady state in betaN, li and rotation, the classical tearing stability index Delta’r0 in DIII-D may evolve slowly. IBS discharges (ITER similar shape, H-mode with ELMs and sawteeth, betaN~2 and q95~3) were run with 1 msec faster resolution CER (standard 5 msec) of toroidal and poloidal rotations. Discharges can exhibit a rotating m/n=2/1 magnetic perturbation, in response to sequential ELMs and sawteeth, that evolves from marginal to robust growth into an eventual locked mode and disruption. Key conditions for algebraic linear temporal growth include an MHD-induced transient with a large enough magnetic perturbation Brms and mode rotation change. Figures 1 and 2 show analyses of NTM seeding events with the fast CER that have been examined in greatest detail, among the multiple discharge broader database.
The key stabilizing factor depends on the relative rotation [parameterized by a gate function F(fm)≤1] between the mode rotation frequency fm and the Er=0 frame of the plasma fE being non-zero but not more than that of the (positive in DIII-D) ion diamagnetic mode frequency f*i ~ 1 kHz in Figs. 1 and 2. The mode island width growth rate dw/dt is modeled with a modified Rutherford equation (MRE) along with models for changes in both mode and plasma rotation:
$\begin{equation} \frac{dw}{dt}=D_{\eta}\left[\frac{d_{NTM}}{w}-\frac{w^2_{pol}}{w^3}F(f_m)\right],\;\;F(f_m) \equiv -4\frac{(f_m-f_E)(f_m-f_E-f_{*i})}{f^2_{*i}} \;\;\;\;\;\;\;\;\;\; \end{equation}$
Here, the classical tearing stability index is negligible, i.e., Delta’r0=-0.1. The critical island for growth is w0=wpol(F/dNTM)1/2 where dNTM is bootstrap drive and wpol is 2X the ion banana width wib. A toroidal adaptation of recent slab-model theory (Beidler 2018) predicts MHD transients abruptly induce a 2/1 tearing response, radially local torque δJ_∥ δB_x, radial electric field and flows that reduce the relative mode frequency. The mode rotation dynamics is described by
$\begin{equation} \frac{df_m}{dt}\cong-\frac{f_m-f_t}{\tau_\zeta}-\frac{f_m-f_E}{\tau_w}+\delta J_\parallel\delta B_x,\;\; \tau_\zeta\cong\frac{a^2_{eff}}{4D_\mu},\;\;\frac{1}{\tau_w}\cong C_w\frac{v_{Ti}}{Rq}\frac{w}{r_0} \;\;\;\;\;\;\;\;\;\; \end{equation}$
Fits to experimental data (for an ELM-induced NTM in Fig. 1 as an example) capture the experimental behavior (pink lines in Fig. 1) of evolution from marginal to robust 2/1 growth. The stabilizing gate factor F depends on the relative rotation and plunges during an ELM, either recovering or remaining down for large enough mode amplitude. In addition to theory, the NIMROD code is used to study evolution at the 2/1 surface in response to an ELM. The code uses an extended MHD model with heuristic closures to model the electron and ion neoclassical parallel stresses. NIMROD indicates the Fig. 1 DIII-D equilibrium is stable to classical tearing modes but a pulsed MHD perturbation at the computational boundary can kick off a 2/1 mode.
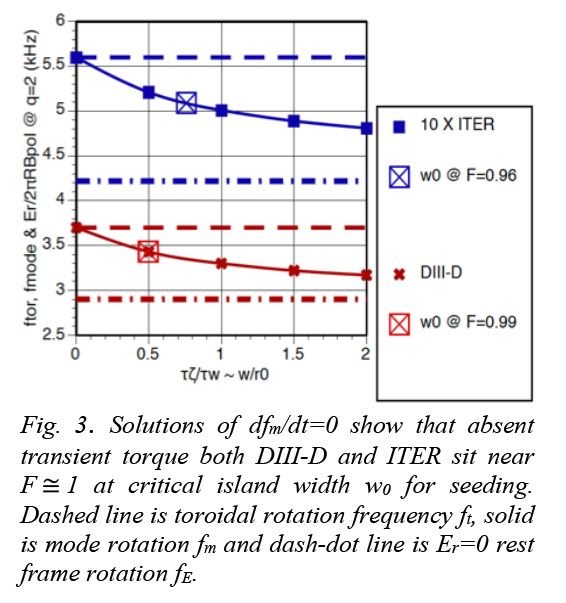
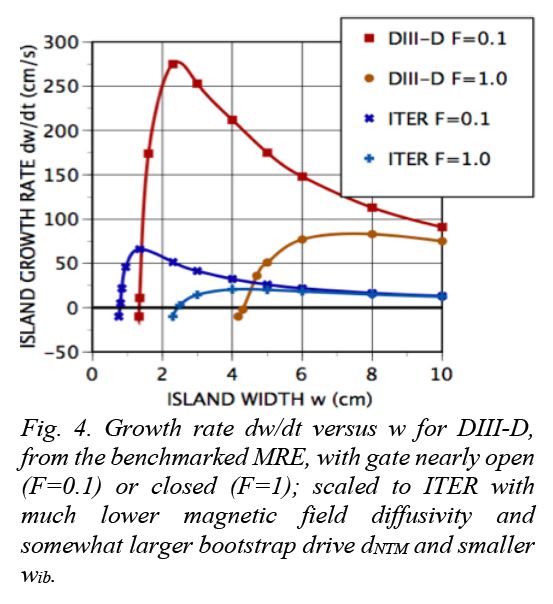
Applying a MHD transient torque to the situation in Fig. 3 can drive relative rotation down and open the gate, as in Fig. 4. The predicted island growth rate in ITER is slower due to its much smaller magnetic field diffusivity but shifted to smaller w0 and very much smaller (0.1X) relative size w0/r0. The IBS equilibrium in DIII-D is very similar to what is modeled (Polevoi 2006, 2019) for ITER. Similar j and q profiles imply comparable classical tearing stability Delta’r0=-0.1 in ITER which is neglected in the MRE of Eq. 1. The ratio of q=2 bootstrap to equilibrium current density (~d_NTM) is also similar. At critical island w0 for F≅1, DIII-D mode rotation fm is about 0.5Xfi=0.6 kHz above fE (Fig. 3); ITER is similar with fi of 0.165 kHz.
This new work gives experimental and theoretical insights, as well as novel benchmarked toroidal theory-based modeling, to a longstanding uncertainty in projecting how NTMs are triggered (Buttery 2007, Hender 2007) for scaling to ITER and beyond. It also provides the framework (e.g., for real-time monitoring) to develop criteria for transient-MHD-induced excitation and robust growth of 2/1 NTMs that can lead to problematic locked modes and disruptions in burning plasma tokamaks, and for which experimental data is limited.
This work was supported in part by the US DOE under DE-FC02-04ER54698.
| Affiliation | General Atomics |
|---|---|
| Country or International Organization | United States |
