Speaker
Description
One of the most interesting open questions of plasma physics is the formation of mean or large scale magnetic field from random or short scale fluctuations of plasma flows.It is believed that generation of large and intermediate scale magnetic fields via the nonlinear energy transfer from kinetic to magnetic modes through continuously stretching and refolding the magnetic field lines is one of the key mechanism for mean field generation [1]. In this work, perhaps for the first time, using a self-consistent single fluid compressible 3D MHD model, numerical study is performed with ABC flow as the velocity field at various forcing scales. Quasi-steady state turbulent spectra of kinetic and magnetic energies are obtained at high resolution. Our results when compared with earlier kinematic dynamo studies [2], show existence of novel saturation mechanis.
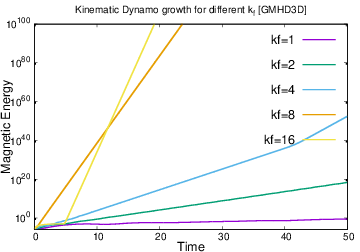
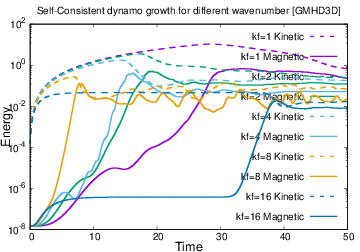
The phenomenon of magnetic energy growing exponentially with time for a statistically steady flow, where the velocity field is held fixed in time or driven, is called, kinematic dynamo action. It is now established that if a ABC flow [3] is used as the driving flow field, in the presence of a certain class of sub-grid scale turbulence models defined by a spectrally dependent viscosity $\nu(k)$, a kinematic dynamo has an optimum drive scale $k_f$ [2]. It is known that at smallest wave number [i.e,$k_fL = 1$] the laminar critical magnetic Reynolds number $Rm_c^{lam}$ is more than an order of magnitude smaller than the turbulent critical magnetic Reynolds number $Rm_c^{turb}$, due to hindering effect of turbulent fluctuations. In a recent study it was shown that for kinematic dynamo with ABC flow, the turbulent $Rm_c^{turb}$ is minimum for $k_fL = 4$ [2]. An important question that is yet to be fully answered is, for the same flow type, what would happen if the back-reaction of the magnetic field, influences the flow field? In this case, Is there an optimal $k_f$ for “self-consistent” dynamo? How does the dynamo action depend on $\nu(k)$? What are the saturation mechanisms in a self-consistent dynamo? To address some of these issues, we have first developed a fully nonlinear, 3D, scalable, compressible, MHD OpenMP solver [3]. Results for ABC-type flow is shown for $N = 64^3$ for both Kinematic and Self-consistent cases in Fig : 1 and 2. This code has been upgraded to a fully multi-node, multi-GPU Solver GMHD3D. Using the new solver, we study the effect of ABC like flows for 3D grid size N = $64^3$, $128^3$, $256^3$, $512^3$ and have addressed several important issues discussed early on, the details of which will be presented.
Referencess:
-
H Moffatt, Cambridge University Press, Cambridge, London, New York, Melbourne, 1978.
-
M Sadek, A Alexakis, and S Fauve, Physical Review Letters, 116(7):074501, 2016.
-
R Mukherjee, HBNI PhD Thesis 2019, IPR, India.
-
R Mukherjee, R Ganesh (2019), arXiv preprint arXiv:1901.09610.
-
R Mukherjee, R Ganesh, V Saini, U Maurya, N Vydyanathan, B Sharma, (2018, December), In 2018 IEEE 25th International Conference on High Performance Computing Workshops (HiPCW) (pp. 46-55). IEEE.}
| Affiliation | Institute for Plasma Research |
|---|---|
| Country or International Organization | India |
