Speaker
Description
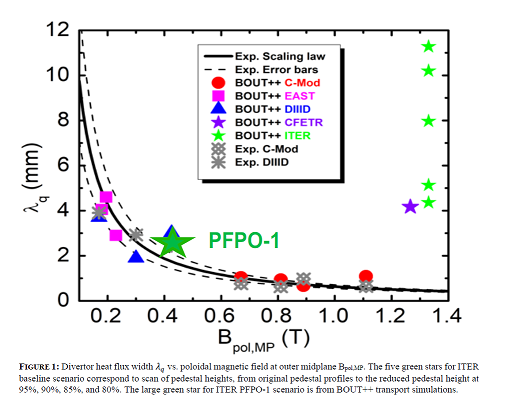
The BOUT++ simulations of C-Mod, DIII-D, and EAST H-mode discharges follow the Heuristic-Drift-based (HD) empirical divertor heat flux width scaling of the inverse dependence on the poloidal magnetic field [1,2]. The BOUT++ simulations for ITER and CFETR indicate that divertor heat flux width $\lambda_q$ of the future large machines may no longer follow the $1/B_{pol,OMP}$ scaling, while the HD model gives a pessimistic limit of divertor heat flux width as shown in Fig.1. The simulation results show a transition from a drift dominant regime to a fluctuation dominant regime from current machines to future large machines such as ITER and CFETR [3]. A threshold formula of thermal transport is derived for a transition from drift dominant regime to fluctuation dominant regime
$$\chi_\perp^c=C {2T_{e,sep}^{3/2}\over BB_p R} {m_p^{1/2}\over e^2} {a\over R},$$
where C=26.5 is a fitting parameter to simulations for the transition. When $\chi_\perp\ll\chi_\perp^c$, the heat flux width $\lambda_q$ is a constant, the drifts dominate cross-field transport and heat flux width is insensitive to the turbulent transport $\chi$, which is consistent with the Goldston HD model. When $\chi_\perp \gg<\chi_\perp^c$, heat flux width $\lambda_q$ increases with $\chi$, corresponding to fluctuation dominating cross-field transport. The threshold formula indicates two reasons for the transition. (1) The magnetic drift-based radial transport decreases due to large CFETR and ITER machine sizes and strong magnetic field. (2) The SOL fluctuation-driven thermal diffusivity increases due to larger turbulent fluxes ejected from the pedestal into the SOL when operating in a small and grassy ELM regime. The formula further indicates that by fixing the safety factor $q_{95}$, the separatrix temperature $T_{e,sep}$, the inverse aspect ratio (a/R), and the machine size R, the critical value of thermal diffusivity $\chi_\perp^c$ is inversely proportional to the square of the poloidal magnetic field $B_{p}$($\chi_\perp^c≈1/B_p^2$). Therefore, a reduction of poloidal magnetic field or plasma current by a factor of 3 from ITER baseline target scenario would lead to a 9 times higher critical value of thermal diffusivity $\chi_\perp^c$, possibly yielding a transition from fluctuation to drift dominant regime. BOUT++ transport simulations confirm the analytical estimate for the transition, as shown in Fig.1 as a large green star for $B_{pol,MP}=0.42T$. More BOUT++ ITER turbulence simulations will be presented to confirm the transitions for the ITER scenarios in Pre-Fusion Power Operations, such as PFPO-1 and PFPO-2, and Steady State Operation.
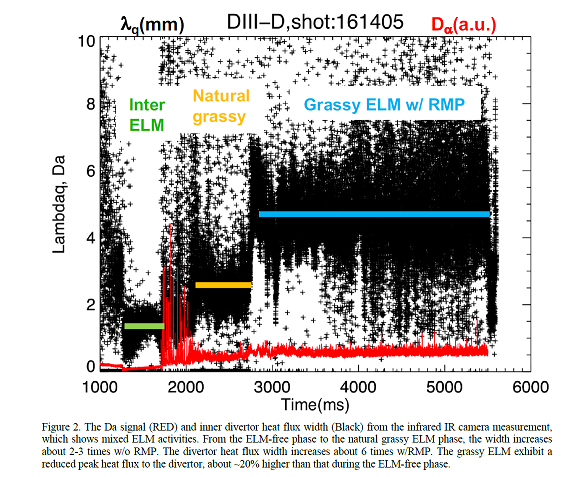
Even for present tokamaks, there is evidence that the divertor heat flux width can have a significant departure from the HD model and the empirical scaling predictions. Recent DIII-D grassy ELM experiments show a consistent divertor heat flux width broadening and amplitude reduction on the inner target [4], as predicted by BOUT++ simulations. From the ELM-free phase to the grassy ELM phase with RMP, the time-averaged divertor heat flux width increases up to 6 times, while the divertor heat flux width features strong fluctuations during the type-I intra-ELM phase. The natural grassy-ELMs with the no-RMP case show a similar broadening with 2-3 times divertor heat flux width in the ELM-free phase. The excitement about the grassy-ELM regime is that the global confinement is maintained and the peak heat flux at the divertor targets is reduced by a factor of 10 in comparison with type-I ELMs as demonstrated in EAST, JT-60U, and TCV experiments. Recent linear and nonlinear BOUT++ simulations on EAST experiments have revealed, for the first time, that the key mechanism for the grassy ELMs is the expansion of the peeling boundary into a stable region due to radially localized steepening in the pedestal pressure gradient triggered by a radially localized collapse [5], based on the well-known effect of kink/peeling mode stabilization by pressure gradient. For type-I ELMs, the high current density and gradient drive the kink/peeling-dominated low-n PBMs instability. During ELM crash cases, the collapsing front propagates radially inward, leading to large ELMs, as observed by the Lithium BES on EAST. For grassy ELMs, the pedestal current density and gradient are inherently lower, and the operational parameter space can intrinsically improve the pedestal stability against the low-n PBMs. Hence, the instabilities quickly dissipate as the pressure gradient is just slightly reduced, leading to small ELMs.
The grassy ELM regime is particularly suited for a high magnetic field steady-state tokamak reactor, such as the CFETR with $q_{95}$ = 5.5-7, $\beta_p$=2, $f_{GW}\simeq 0.7-1.2$, $\delta_{95}\simeq 0.4-0.5$, and $\nu_{*ped}\le 0.3-0.8$ [6]. Even though the ITER baseline operation scenario is in the type-I ELMy H-mode regime for the highest fusion power with the highest current and the highest pedestal temperature, the parameters for ITER steady-state operation scenario with lower current ($q_{95} = 5.3, \beta_p=1.65, f_{GW}\simeq 0.82, \delta_{95}\simeq 0.5$) are in principle consistent with those for achieving the grassy ELMs. BOUT++ six-field two-fluid turbulence code is applied for simulations of different ITER scenarios, namely 15 MA baseline, 11.5MA hybrid and 10MA SSO (Steady-State Operation). The most unstable modes in linear stage show that different peeling-ballooning instabilities dominate in the three scenarios, with the baseline scenario has the most unstable toroidal mode numbers in the range of n=60~80 with characteristics of ballooning modes, the hybrid scenario has the most unstable modes at n~40, and for the SSO scenario the most unstable modes are in the range of n=15~20 with characteristics of peeling modes. The nonlinear simulations yield different types of ELMs in the final nonlinear phases. The energy loss fractions in the baseline and hybrid scenarios are large (~10-20%) while the one in the SSO scenario is dramatically smaller , which are consistent with the features of type-I ELMs and grassy ELMs respectively. The divertor heat flux widths in the three scenarios are larger than the estimations based on the Eich’s scaling [1,2]. This may be explained by the anomalous thermal diffusivities that exceed the threshold between the drift dominant regime and fluctuation dominant regime [3], i.e., the divertor heat flux can be broadened by strong fluctuation in grassy ELM regime. The ITER tungsten divertor targets have mono-block structure with shaping, and the melting limit of toroidal edge of the mono-block is about 3 times lower than that of surface [7]. The toroidal gap edge melting limit of tungsten imposes constrains on ELM energy loss fraction, which depends on pedestal height, machine size, divertor heat flux width, and incident angle of magnetic field on divertor targets. The analytical estimates show that the ELM energy loss fraction ($\Delta W/W_{ped}$) should be smaller than 0.74%, 1.19%, and 2.03% for ITER baseline target, hybrid and SSO scenarios, respectively. The combination of small grassy ELM energy loss fraction ($\Delta W/W_{ped}< 0.1-1%$ [8]) and broadened foot print makes the SSO with grassy ELMs a highly promising operational scenario, satisfying the constraints on divertor material.
[1.] Goldston R.J. 2012 Nucl. Fusion 52 013009; [2.] Eich T. et al Nucl. Fusion 53 (2013) 093031; [3] X.Q. Xu, et al Nucl. Fusion 59 (2019) 126039; [4] Nazikian, et al. Nucl. Fusion 58 (2018) 106010; [5] G S Xu, et al., Phys. Rev. Lett. 122, 255001 (2019); [6] E. Viezzer, Nucl. Fusion, vol. 58, 115002 (2018). [7] J.P. Gunn, et al Nucl. Fusion 57 (2017) 046025. [8] N. Oyama, Journal of Physics: Conference Series 123 (2008) 012002.
| Affiliation | Lawrence Livermore National Laboratory |
|---|---|
| Country or International Organization | United States |
