Speaker
Description
In addition to the existing hybrid electromagnetic (EM) scheme that uses gyrokinetic ions and fluid electrons (Ref. 1), two new EM schemes, which use kinetic electrons, have been implemented in the whole-volume particle-in-cell (PIC) code XGC (Ref. 2). In particular, these new EM schemes in XGC will allow higher-fidelity global simulation of long-wavelength modes, which are important for studying the onset of edge localized modes (ELMs) and their interaction with micro-turbulence and neoclassical dynamics, and also ELM control, via resonant magnetic perturbations (RMPs) and other means. Additionally, EM effects for XGC-focused ITER problems, such as divertor heat-load width, L-H and H-L transitions, pedestal height and shape, and RMP penetration, should include long-wavelength modes self-consistently with other physics effects. Traditionally, the PIC approach exhibited higher numerical sensitivity to the so-called "cancellation problem" (Ref. 3) at long wavelengths than the continuum approach.
The first new kinetic-electron EM scheme that has been implemented in XGC is a fully implicit numerical scheme (Ref. 4) that uses the symplectic formulation of gyrokinetics. The second new scheme that has been implemented is an explicit numerical scheme (Ref. 5) that uses the Hamiltonian formulation of gyrokinetics. Both the implicit and explicit numerical schemes have significant advantages over each other that make both viable for consideration, depending on the particular physics of interest and computational architecture. For example, the implicit scheme completely avoids the numerical cancellation problem that has to be mitigated in the explicit scheme (Ref. 5), whereas, the explicit scheme has a simpler numerical implementation and better performance in general. Our ability to rigorously evaluate these two numerical schemes is, therefore, an important aspect of this work.
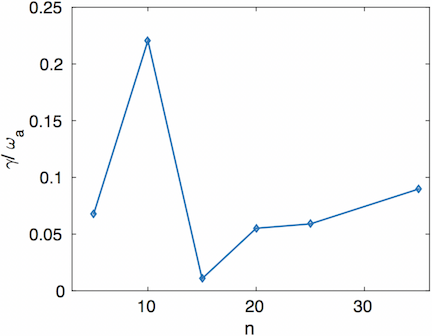
The verification of the hybrid EM scheme in XGC was presented in Ref. 1. The hybrid EM scheme, which does not suffer from the cancellation problem, showed that kinetic ballooning modes (KBMs) in NSTX are generally stable in the pedestal region, but could be unstable at the pedestal top, and that the low-$n$ peeling modes generally exist in the steep gradient region of DIII-D and KSTAR pedestals, without a sharp instability boundary, which are contrary to the usual MHD results. We see gyrokinetic peeling modes at low $n<15$ and electromagnetic ITG modes at higher $n>15$, as shown in Figure 1. It appears that the gyrokinetic peeling modes require interaction with mean $E\times B$ shearing and microturbulence to be nonlinearly unstable.
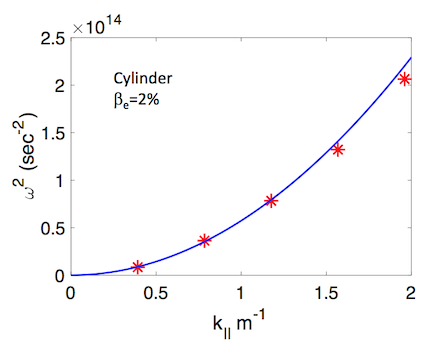
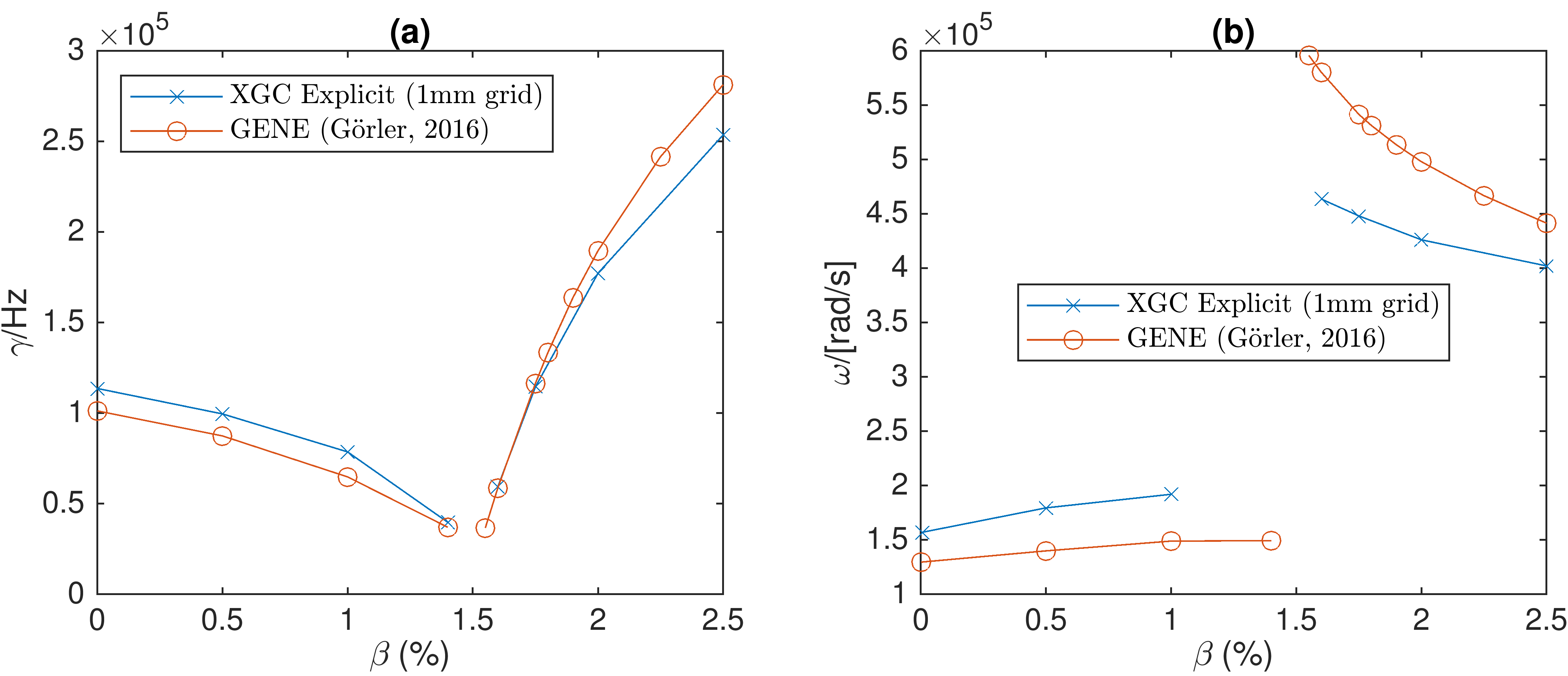
The verification of the new implicit and explicit numerical schemes has been performed for shear-Alfvén modes, as well as the ion temperature gradient (ITG) to KBM transition at finite plasma $\beta$ (Ref. 6). Verification results for shear-Alfvén modes with the implicit scheme are shown in Figure 2. Performing such verification simulations with the explicit scheme would be particularly challenging because of the cancellation problem. Verification results for the ITG-KBM transition for the explicit Hamiltonian scheme are shown in Figure 3, with the cancellation problem successfully mitigated. The stabilization of the ITG instability from 0% to 1.5% plasma $\beta$ is reproduced, and there is good quantitative agreement with the GENE code (Ref. 6). The ITG to KBM transition is also reproduced, and there is again good quantitative agreement with the GENE code for the destabilization of the KBM above 1.5% plasma $\beta$.
Some results from electromagnetic studies of critical ITER edge physics, such as divertor heat-load width, L-H transition, pedestal structure, and ELM onset and RMP control, will be presented.
References:
- R. Hager, J. Lang, C. S. Chang, S. Ku, Y. Chen, S. E. Parker, and M. F. Adams, Phys. Plasmas 24, 054508 (2017);
- S. Ku, C. S. Chang, R. Hager, R. M. Churchill, G. R. Tynan, I. Cziegler, M. Greenwald, J. Hughes, S. E. Parker, M. F. Adams, E. D’Azevedo, and P. Worley, Phys. Plasmas 25, 056107 (2018);
- Y. Chen and S. Parker, Phys. Plasmas 8, 441 (2001);
- G. Chen and L. Chacón, Comput. Phys. Commun. 197 (2015) 73–87;
- A. Mishchenko, R. Hatzky, and A. Könies, Phys. Plasmas 11, 5480 (2004);
- T. Görler, N. Tronko, W. A. Hornsby, A. Bottino, R. Kleiber, C. Norscini, V. Grandgirard, F. Jenko, and E. Sonnendrücker, Phys. Plasmas 23, 072503 (2016).
| Affiliation | Princeton Plasma Physics Laboratory |
|---|---|
| Country or International Organization | United States |
