Speaker
Description
The pedestal plays an important role in determining the confinement in tokamak H-mode plasmas. However, the steep pressure gradients in this transport barrier also lead to edge localized modes (ELMs) 1. There is good understanding of the pedestal in type I ELM regimes [2], however, type I ELMs are known to damage plasma facing components and so future large tokamaks must operate with small or no ELMs [3]. We aim to develop a capability to predict the pedestal heights for these regimes based on an improved understanding of the underlying pedestal physics.
We have analysed JET data which shows that Quiescent H-mode (QH-mode) often occurs at low collisionality, Fig. 1.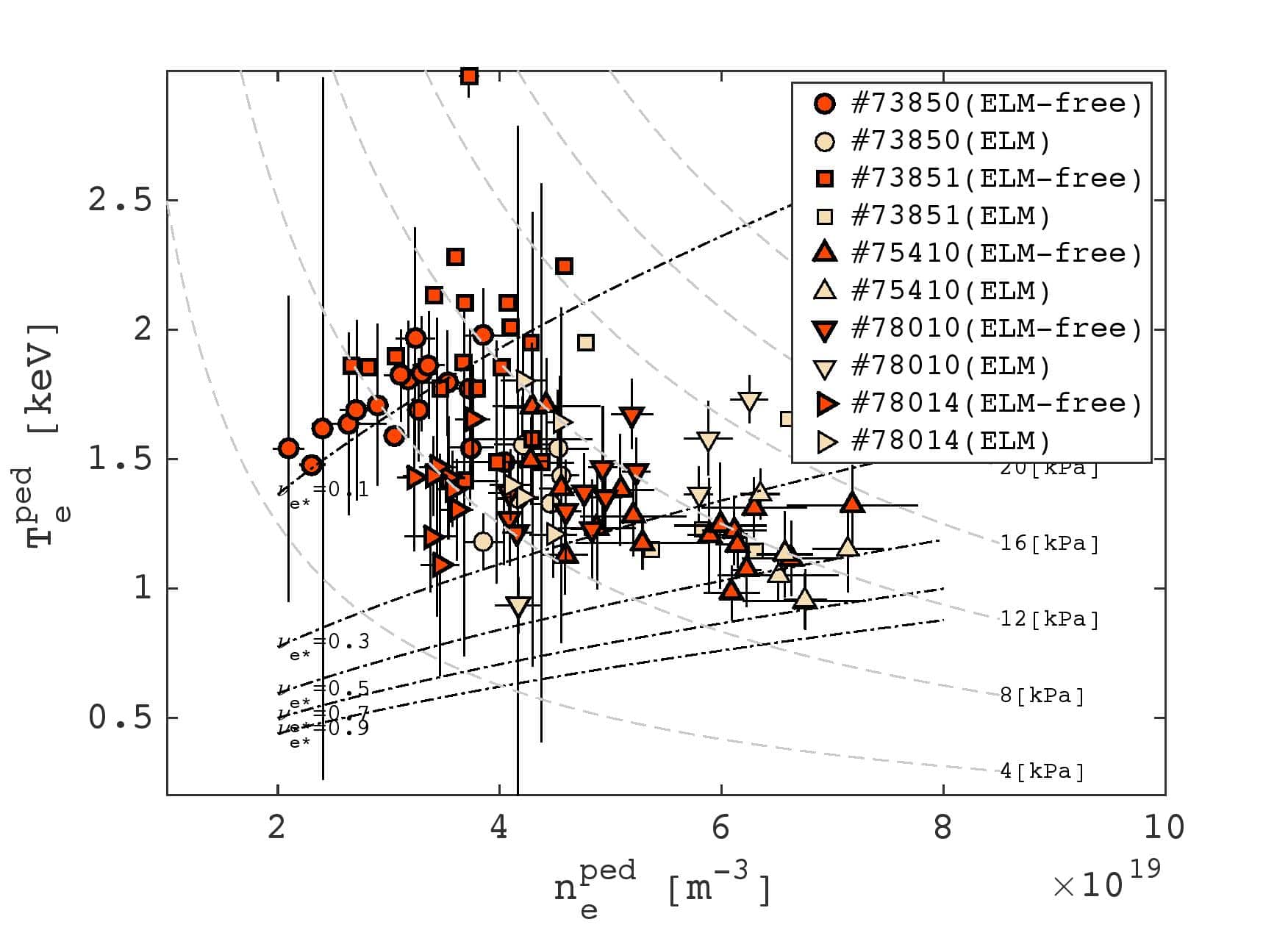 
This indicates that QH-mode may be produced by a pressure driven mode which drives a strong pedestal bootstrap current at low collisionality, flattening the safety factor profile. QH-mode is ELM free and characterised by an edge harmonic oscillation (EHO) which is the signature of a saturated MHD mode with low toroidal mode number, n, that prevents the pedestal from reaching the ELM stability limit [4,5]. The VMEC [6] non-axisymmetric equilibrium code has been used to find saturated equilibria which qualitatively match the QH-mode [7] with different types of safety factor profiles. A pressure driven saturated state where the bootstrap current flattens the safety factor profile near a rational value at the edge of the plasma has been found [8]. We have also understood the mode structure of this saturated state [9]. Linear ballooning mode calculations show that certain toroidally localized regions of the plasma have become more unstable. These MHD modes may provide the extra density transport required to avoid the pedestal reaching the ELM instability limit [10]. We will also assess what gyrokinetic or other calculations will be required to make pedestal height predictions for QH mode plasmas.
We have shown that the Hager and Sauter bootstrap formulae agree with the ELMFIRE [11] code without Shafranov Shift. The bootstrap current makes an important contribution to the stability of the plasma as it alters the current profile and affects current driven instability and the q profile. The numerical calculation of the bootstrap current in the pedestal requires a full-f code and here we use the code ELMFIRE. Formulae such as those produced by Sauter and Hager [12] are often used in calculations but these are idealisations. The comparison between ELMFIRE results and the Hager and Sauter formulae agree in a regime without the Shafranov Shift, but differ due to Shafranov Shift effects. We will also test the effects of turbulence on the bootstrap current using ELMFIRE and report this work.
Small ELM regimes such as type II and type III ELMs also lack detailed understanding and a way of predicting the pedestal height. We are looking at type III ELMs using the MHD stability code MARS-F [13] which has been demonstrated to run in a restricted region around the pedestal. MARS includes resistivity and plasma flow and the significance of these attributes will be investigated. We have also carried out preliminary work using gyrofluid simulations of small ELMs using the BOUT++ framework [14]. It has been demonstrated theoretically and numerically that a given linear toroidal drift mode has two distinct classes of structure with different stability limits. These are known as the isolated and general modes. The isolated class balloons at the outboard midplane whilst the general mode peaks away from this point. The interaction of these modes is postulated as a possible cause of Grassy ELMs [15]. Type II ELMs will also be investigated using the nonlinear ballooning framework of Ham and Cowley [16] by scans in plasma shape from lower single null to connected double null.
We have started investigation of the effect of density not being a flux surface function on the MHD stability of the pedestal plasma using linear JOREK [17] runs and prescribed plasma density. We will extend this to nonlinear ELM simulations if we see an effect. We are also analytically calculating the bootstrap current assuming a simple dependence of density with poloidal angle. These results will help us decide if we need to model the pedestal including poloidal variation of density.
The final aspect of the work is to improve our method of pedestal height predictions for type I ELMs. This will provide a key insight for predicting pedestal heights for the small ELM regimes. Current pedestal prediction frameworks, such as EPED, find the pressure pedestal height and width but require the density pedestal height and global plasma beta. In a truly predictive model of the pedestal these two inputs must be calculated self-consistently. We have developed a framework in which we will use quasi-linear estimates of the turbulent heat flux to constrain the density and temperature profiles to match a given input power. We draw on results from theoretical [10] and experimental [18] analysis to propose simple models for the temperature and density pedestals.
References
1 C J Ham et al., Nature Reviews Physics ‘Filamentary plasma eruptions and their control on the route to fusion energy’ Accepted (2020); [2] P B Snyder et al., Nucl. Fusion 51 103016 (2011)
[3] R A Pitts et al., Nuclear Materials and Energy 20 100696 (2019); [4] K H Burrell et al., Phys. Plasmas 23 056103 (2016); [5] E R Solano Phys. Rev. Lett. 104 185003 (2010) [6] S P Hirshman & J C Whitson, Phys. Fluids 26 3553 (1983); [7] J P Graves, 9th International Workshop on Stochasticity in fusion plasmas “Linear and nonlinear analytical and numerical calculations of edge harmonic oscillations in ELM-free H mode plasmas” (2019); [8] D. Brunetti et al., Nucl. Fusion 58 014002 (2018); [9] A Kleiner et al., Plasma Phys. Control. Fusion 61 084005 (2019); [10] M Kotschenreuther et al., Nucl. Fusion 59 096001 (2019); [11] J.A.Heikkinen et al., J. Comp. Phys. 227 5582 (2008); [12] R. Hager et al., Phys. Plasmas 23 (2016) 042503; [13] Y Q Liu et al., Phys. Plasmas 7 3681 (2000); [14] B D Dudson, et al., Plasma Phys. Control. Fusion 53 054005 (2011); [15] A Bokshi et al., Plasma Phys. Control. Fusion 58 075011 (2016); [16] C J Ham et al., Plasma Phys. Control. Fusion 60 075017 (2018); [17] G T A Huysmans, & O Czarny, Nucl. Fusion 47, 659-666 (2007); [18] A Field et al., Plasma Phys. Control. Fusion 62 (2020) submitted.
| Affiliation | UKAEA-CCFE |
|---|---|
| Country or International Organization | United Kingdom |
