Speaker
Description
In drift-wave turbulence, cross-correlations between fluctuations produce turbulent fluxes, which have profound consequences for confinement and the underlying nonlinear turbulence dynamics. In this work, we use a new approach based on deep learning to obtain a reduced mean-field model for the drift-wave/zonal flow dynamics from simulations of the Hasegawa-Wakatani system. In particular, we uncover a non-diffusive particle flux driven by the vorticity gradient, which is a new mechanism for corrugation of the profile. In this system, this effect is stronger than that of the shear. The new method also explicitly recovers previous analytical models for zonal flow generation, based on negative viscosity.
Reduced models of turbulence and transport are essential to the predictive understanding of plasma profile formation. A useful reduced model should distill the essential physics understanding gleaned from large scale simulations and also enable wide-ranging explorations of parameter space. The key physics of anomalous transport, flow generation (and other structure formation processes), and virtually all aspects of the turbulent transport dynamics is ultimately encoded in the turbulent fluxes. Such fluxes are enabled by finite cross-correlations (cross-phases) between fluctuating quantities; computing these cross correlations is the central problem in plasma turbulence modeling. However, such calculations are challenging, since they require the use of several, frequently debatable, approximations.
In this work, we introduce a novel data-driven approach to determine the dependencies of the cross-correlations. The new method uses deep supervised learning to infer a mean-field model from numerical solution and/or experiment. This approach, a form of nonparametric regression, leverages deep learning’s resilience to the large amounts of noise inherent to turbulence, as well as its ability to model arbitrary nonlinear, multivariate functions.
As a test of concept, we numerically solve the 2-D Hasegawa-Wakatani (HW) system, and use computed mean field quantities to train a deep neural network (DNN) which outputs the local turbulent particle flux and Reynolds stress as a function of local mean gradients, flow properties, and turbulence intensity. Exact symmetries are exploited to select independent variables and constrain the model. Up to nonlinear saturation effects, the DNN infers a model for the turbulent particle flux of the form $\langle \tilde v_r \tilde n \rangle \simeq \varepsilon ( - D_n \partial_x n D_u \partial_x u)$ where $\varepsilon$ is the turbulence intensity, $n$ and $u$ are respectively the mean density and vorticity, and $D_n$ and $D_u$ are constants. The first term is the familiar quasilinear diffusion which tends to relax the driving gradient. The second, proportional to the gradient of vorticity (see Fig. 1), is non-diffusive and previously unreported. We recover this non-diffusive flux with a simple analytic calculation. Notably, the deep neural network finds that, in this system, the vorticity gradient effect on the particle flux is significant, and much stronger than the direct effect of the local vorticity (shear).

The non-diffusive flux originates from a shift in the drift-wave frequency induced by the nonlinear convection of vorticity. It has immediate implications for structure formation, as it tends to modulate the density profile in the presence of a quasiperiodic zonal flow, forming a staircase. This mechanism for staircase formation is independent from previous models based upon bistability. We show that the same shift in the drift-wave frequency also impacts the local linear growth rate, resulting in corrugations in the intensity profile localized where the density and vorticity gradients have the same sign.
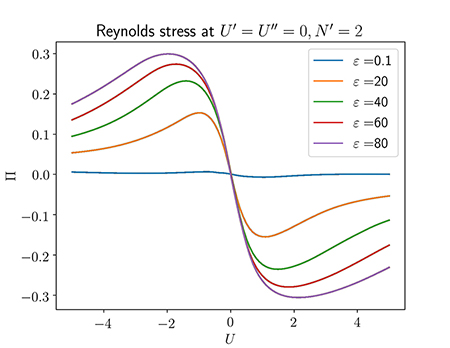
Using the new method, we also uncover a Cahn-Hilliard-type model for the generation of zonal flow via Reynolds stress, which agrees with and finds corrections to previous theoretical work 2. Explicitly, we find at leading order $\langle \tilde v_r \tilde v_\theta \rangle \simeq \varepsilon (-\chi_1 u+\chi_3 u^3-\chi_4 \partial_x^2 u)$ (see Fig. 2). The recovery of the small, but important hyperviscous term shows that the deep learning approach passes a sensitive test.
Finally, the learned models for the particle flux and Reynolds stress are combined with conservation of potential enstrophy, similar to [3], to form a 3-field, 1-D reduced model for the turbulent dynamics. This system is solved numerically. The solution of the simplified model correctly exhibits several features of the nonlinear dynamics of 2-D HW, including the spontaneous formation and stabilization of zonal flows, the modulation of the density profile, and the formation of corrugations in the turbulence intensity.
While the 2-D HW system is a simple and computationally inexpensive example, our results suggest that the deep learning method can possibly be applied to other, more complex applications, such as more sophisticated reduced models, gyrokinetic simulations, or even experiment. This analysis thus opens a new avenue for model reduction, which circumvents some of the analytic intractability of such models. We speculate that training is likely to succeed if (a) the system exhibits a requisite degree of symmetry, (b) a finite set of important mean-field variables can be identified, and (c) data can be obtained spanning a broad range of those variables. Exact symmetries are especially useful, as model constraints. However, the underlying assumption of a mean-field model is valid only in the weak turbulence regime and breaks down when the dynamics become sufficiently intermittent. Moreover, the assumption of locality in space and time is a significant, ad hoc limitation.
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation. It was supported by the U.S. Department of Energy.
References:
1 R. Numata, R. Ball, and R. L. Dewar. Phys. Plasmas 14, 102312 (2007).
2 P. H. Diamond, S.-I. Itoh, K. Itoh, and T.S. Hahm. Plasma Phys. Control. Fusion 47, R35 (2005).
[3] A. Ashourvan and P. H. Diamond. Phys. Plasmas 24, 012305 (2017).
| Affiliation | UCSD |
|---|---|
| Country or International Organization | United States |
