Speaker
Description
In this paper, we present a novel approach to simulate plasma turbulence in tokamak geometry. Even with most advanced supercomputers in these days, it is still very challenging to simulate turbulence and transport globally in the realistic tokamak geometry. One of challenges is the time scale disparity between ion and electron due to the large mass ratio between them.
We propose a new kinetic-fluid hybrid model to simulate ion scale electromagnetic turbulence (i.e. fluctuations with $k_\perp \rho_i \le 1$) in efficient ways retaining essential kinetic electron physics. All ionic species are modeled by gyrokinetic equations. The evolution of electron density perturbation $\delta n_e$ is described by the fluid continuity equation. Perpendicular and parallel pressure are divided into the contributions from passing and trapped electrons as $\delta P_{e\perp,\parallel} = \delta P_{e\perp,\parallel}^P + \delta P_{e\perp,\parallel}^T$. For passing electrons, we assume isotropic pressure perturbation only from the density perturbation:
$\delta P_{e\perp}^P = \delta P_{e\parallel}^P = T_{e0} \delta n_e^P = T_{e0} (\delta n_e - \delta n_e^T)$.
The pressures $\delta P_{e\perp,\parallel}^T$ and the density perturbation $\delta n_e^T$ of trapped electrons are evaluated by solving the bounce-averaged kinetic equation:
$\frac{\partial f_e^T}{\partial t} + \frac{d\beta}{dt}\frac{\partial f_e^T}{\partial \beta} + \frac{d\alpha}{dt}\frac{\partial f_e^T}{\partial \alpha} = C(f_e^T) + S^{P,T}.$
Here, $\beta$ and $\alpha$ denote the radial location and toroidal angle of the bounce center of trapped electron at outer mid-plane. $C(f_e^T)$ and $S^{P,T}$ represent operators for the Coulomb collision and the source-sink due to trap-passing population changes. The details of the equations for the bounce motion and the operators can be found in Ref.$[1]$. To describe the evolution of the vector potential, the parallel Ohm’s law for passing electrons is combined with the Faraday’s law.
Though the fluid model alleviates the requirement of time step for the simulation of parallel electron dynamics, the model contains the physics in Alfven time scale, and is still burdensome to simulate with explicit methods. To resolve this, we introduce an Implicit-Explicit (IMEX) Runge-Kutta scheme$^{[2]}$, which separates simulation variables into two groups – those with fast temporal variations and the remaining – and all linear terms and time derivatives of the fluid equations involving the former variables are implicitly discretized. We demonstrate that this IMEX discretization can significantly accelerate the simulations and also resolve the cancellation issue caused by directly evaluating the time derivative of the vector potential $\partial A_{\parallel} / \partial t$. This new hybrid model is implemented in the global gyrokinetic code gKPSP $^{[1]}$.

We demonstrate that the new model allows very efficient simulations of key ion scale instabilities such as ITG, TEM, and KBM. Figure 1 shows linear simulations of ITG and KBM. With a fixed toroidal mode number $n_\varphi=19$, the beta value is changed by increasing the electron density. For low beta values, ITGs are excited, but as the beta increases larger than 1.5%, the mode is changed to KBM. For comparison, global linear GENE simulation results are also plotted$^{[3]}$. We can see that the new model can accurately reproduce the critical $\beta_e$ for the ITG $\rightarrow$ KBM transition, while the growth rates and frequencies of KBM from gKPSP are slightly smaller than those from GENE.

Next, we perform a scan of toroidal mode numbers with a fixed beta value $\beta_e = 1.0\%$. For low toroidal mode numbers, ITGs are excited, but as the mode number increases, ITG<->TEM transition occurs as the result in Figure 2 shows. Again, GENE simulation results with the same conditions are plotted, and we can confirm that the results from the new model agree well with the GENE results.
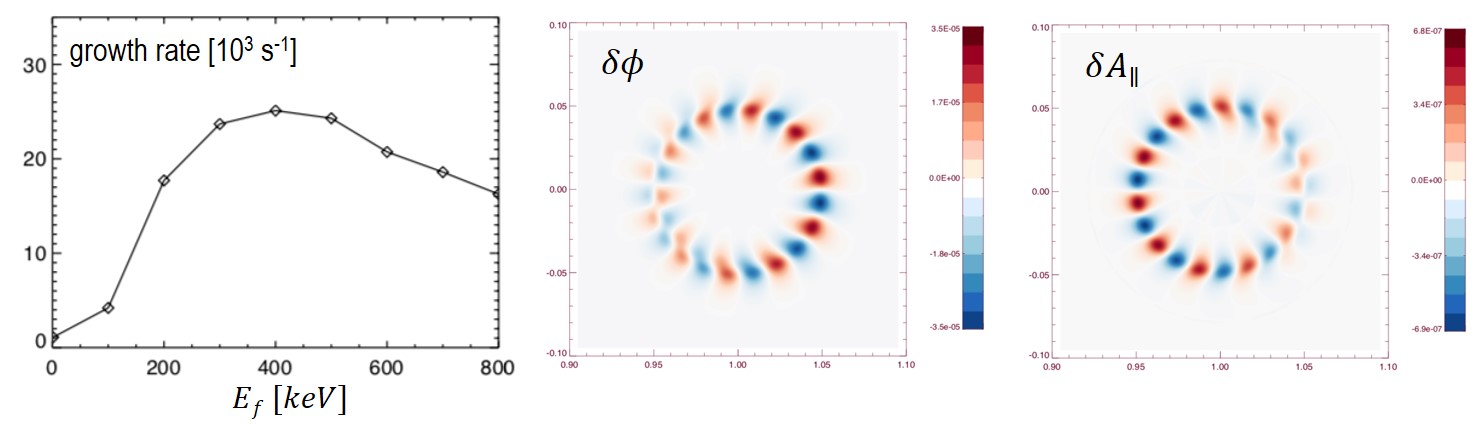
As a final benchmark test, we perform global linear simulations of TAE with energetic ions. We choose the simulation conditions in Ref.$[4]$ for the TAE simulations. Figure 3 shows the growth rates of TAEs driven by varying fast ion energies. The growth rates agree well with the results in Ref.$[4]$. In the figure, the electrostatic and electromagnetic potential are also presented.
From the analysis on computing costs of the new hybrid model, it is found that the overall computing costs for electromagnetic simulation are roughly 5 times of those for electrostatic ITG simulation with adiabatic electrons.
Currently, we are performing global nonlinear simulations using the new hybrid model. We will present that, with the new model, gKPSP can efficiently simulate various global physics of electromagnetic turbulence in realistic tokamak plasma conditions.
References:
$[1]$ J.M. Kwon et al, Comput. Phys. Commun. 177, 775 (2017).
$[2]$ L. Pareschi et al, J. Sci. Comput. 25, 129 (2005).
$[3]$ T. Görler et al, Phys. Plasmas. 23, 072503 (2016).
$[4]$ A. Konies et al, 24th IAEA FEC ITR/P1-34 (2012).
| Affiliation | National Fusion Research Institute |
|---|---|
| Country or International Organization | Korea, Republic of |
