Speaker
Description
The Greenwald density limit ($\bar{n}_g$) defines a fundamental bound on the tokamak operating space, and so is of central importance to magnetic fusion. Recent experiments (1) reinforce the suggestion (2) that the density limit occurs due to an abrupt increase in edge particle transport, with edge cooling and MHD phenomena following as secondary consequences. Here, we present a theory of degraded particle confinement as $\bar{n} \to \bar{n}_g$ due to edge shear layer collapse. The crucial microphysics is a breakdown of the self-regulating turbulence–shear flow feedback loop, due to a drop in flow production. Electron adiabaticity characterizes parameter regimes. Favorable scaling of particle transport and density with current, like the Greenwald $\bar{n} \sim I_p$, emerges from the effect neoclassical screening on zonal flow production. Higher current strengthens zonal flow shear for fixed drive. Zonal flow screening physics has implications for the scaling of the density limit in different devices.
Theoretical work (3) has identified the transition from adiabatic ($\alpha = \frac{k_\parallel^2 V_{th}^2}{\omega \nu} >1$) to hydrodynamic ($\alpha < 1$) electrons with increasing $n$ as a cause of the drop in Reynolds stress-driven production of shear flows, consistent with fluctuation studies close to the density limit (1). These are shown in Fig. 1.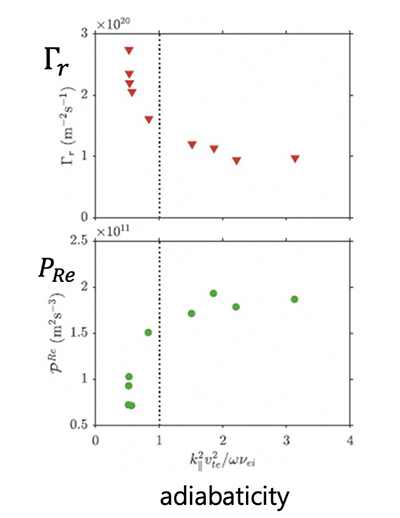 
The physics mechanism is a transition from a regime of propagating drift waves, which generate a flow convergence and so a shear layer spin-up, to one of weakly propagating convective cells, with a consequently weak coherence of $\tilde v_r$ with $\tilde v_\theta$. In the latter, eddy tilting (symptomatic of flow generation) does not arise as a straightforward consequence of causality. Fig. 2 shows the scaling of transport fluxes with $\alpha$. 
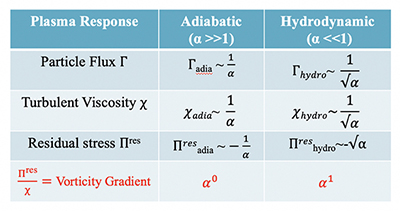Note that the particle flux increases for $\alpha <1$, while the vorticity gradient decreases there. This indicates that self-regulation fails in the hydrodynamic regime. Observe that the vorticity gradient ($\nabla u$) is a natural order parameter for the flow and superior to shear for prediction of suppression, since $\nabla u$ prevents local alignment of eddies with flow shear. Shear layer collapse is consistent with potential vorticity (PV—also total charge) conservation. However, for the $\alpha >1$ regime, PV fluxes of particles and vorticity (i.e. transport and zonal flow) are tightly coupled. For $\alpha <1$, the particles carry the PV flux. Thus, the different regimes manifest different branching ratios of the components of the PV flux, but the same total flux.
Flow–fluctuation–transport feedback is shown in Fig. 3. 
This suggests a unified picture of: the L-mode as a state of modest shear flow, the Density Limit as a state of weak flow, and the H-mode as a state of strong mean shear. The onset of the density limit by shear layer collapse emerges as a transport bifurcation.
Favorable current scaling is a salient feature of the Greenwald Limit. Theoretical work has identified the neoclassical ‘screening’ of the sheared zonal flow (ZF) as the physical mechanism underpinning the favorable $I_p$ scaling. Since the effective ZF scale is set by $\rho_\theta$ (4), effective ZF inertia is lower for larger current. An approximate scaling
$ \tilde v_E^\prime \approx \frac{S_{k,q}}{\rho_i^2 + 1.6 \epsilon^{3/2}_T \rho_{\theta_i}^2} \sim \frac{ \sigma \left(\frac{e \phi}{T} \right)^2_{DW}}{\rho_{\theta_i}^2} \sim \sigma B_\theta ^2 \left(\frac{e \phi}{T} \right)^2_{DW} $
follows. $\left(\frac{e \phi}{T} \right)^2_{DW}$ is the drift wave intensity and $\sigma \sim n^{-\alpha}$ represents production. Higher current strengthens ZF shear, for fixed drive. DW-driven nonlinear noise scales $\sim B_\theta^4$, ensuring persistent excitation of the edge shear layer with increasing $B_\theta$. We see that reduced screening at high $I_p$ can “prop-up” the shear layer vs. weaker production. Favorable current scaling persists in the (ion) banana and plateau regimes, but weakens deep into the Pfirsch–Schlüter regime, also consistent with shear layer collapse at high $n$.
These results have implications for devices other than tokamaks. RFP’s are known to exhibit ‘Greenwald-like’ scaling, as $\bar{n}_g \sim I_p$. This is not surprising, since in RFP $\rho_i$ is set by the poloidal field, i.e. $\rho_i = \rho_{\theta_i i}$, so classical zonal flow screening is weaker (ZF shear stronger) at high $I_p$. In stellarators, the principal correction to classical screening is due to helically trapped particles. This has no obvious length scale (5), so ZF screening is classical. This feature likely explains why attempts to link stellarator density limits to magnetic geometry have failed, and why stellarator density limits appear higher than those in tokamaks.
Ongoing work is concerned with analysis of perturbative experiments of shear layer collapse and with studies of zonal flow evolution in layers with variable $\alpha(r)$. Of particular interest are bias-driven shear studies, which attempt to enhance shear layer persistence beyond $\bar{n}_g$, and elucidate the local dynamics of the density limit.
Research is supported by the U.S. DOE, and CNNC and MOST, China.
(1) R. Hong, et al., Nucl. Fusion 58, 016041 (2018)
(2) M. Greenwald, PPCF 44, 2194 (2002)
(3) R. Hajjar, P.H. Diamond, M. Malkov, PoP 25, 062306 (2018)
(4) M.N. Rosenbluth, F.L. Hinton, Phys. Rev. Lett. 80, 724 (1998)
(5) H. Sugama, T.H. Watanabe, PoP 13, 012501 (2006)
| Affiliation | University of California, San Diego |
|---|---|
| Country or International Organization | United States |
