Speaker
Description
N. Zhang$^1$, Z. C. Yang$^1$, Y. Liu$^1$, Y. Q. Liu$^2$, T. F. Sun$^1$,X. Q. Ji$^1$, P. Piovesan$^3$, V. Igochine$^4$, D. L. Yu$^1$, S. Wang$^1$, G. Q. Dong$^1$, R. Ke$^1$ , J. M. Gao$^1$, W. Deng$^1$, N. Wu$^1$, Q. W. Yang$^1$, M. Xu$^1$ and X. R. Duan$^1$, The HL-2A Team, The ASDEX Upgrade Team and The EUROfusion MST1 Team
$^1$ Southwestern Institute of Physics, P. O. Box 432, Chengdu 610041, China
$^2$ General Atomics, PO Box 85608, San Diego, CA 92186-5608, USA
$^3$ Consorzio RFX, Corso Stati Uniti 4, I-35127 Padova, Italy
$^4$ Max-Planck-Institut fur Plasmaphysik, EURATOM Association, Garching, Germany
Controlling large edge localized modes (ELMs) is critical for tokamaks operating in H-mode, due to potentially severe consequences on material damages caused by ELM bursts in future large scale devices such as ITER $[1]$. Resonant magnetic perturbation (RMP) has been extensively applied to mitigate or suppress ELMs $[2]$. In this work, we report two new recent results on the effect of the $n=1$ ($n$ is the toroidal mode number) RMP fields on ELMs and the associated plasma transport. One is the experimental result on the HL-2A tokamak, where large type-I ELMs were for the first time on this device suppressed by the applied $n=1$ RMP. The other is the toroidal modeling study on the plasma core flow damping by the applied $n=1$ RMP, with computational results quantitatively agreeing with experiments in ASDEX Upgrade $[3]$.
In HL-2A experiments, we find that an increase in turbulence around the pedestal region plays an essential role in the ELM suppression dynamics. The plasma flow damping due to RMP may be a direct cause of the observed increase of turbulence. Figure 1 shows a typical ELM suppression discharge with $4.9 kAt$ current in the coils. The pulse has the toroidal magnetic field of $B_T=1.34$ T and the plasma current of $I_p=120 kA$.The plasma edge safety factor is $q_{95}=3.8$. Within one ELM cycle after switching on the RMP, the large type-I ELM disappears. After the perturbation field is turned off later on in the discharge, large type-I ELMs return.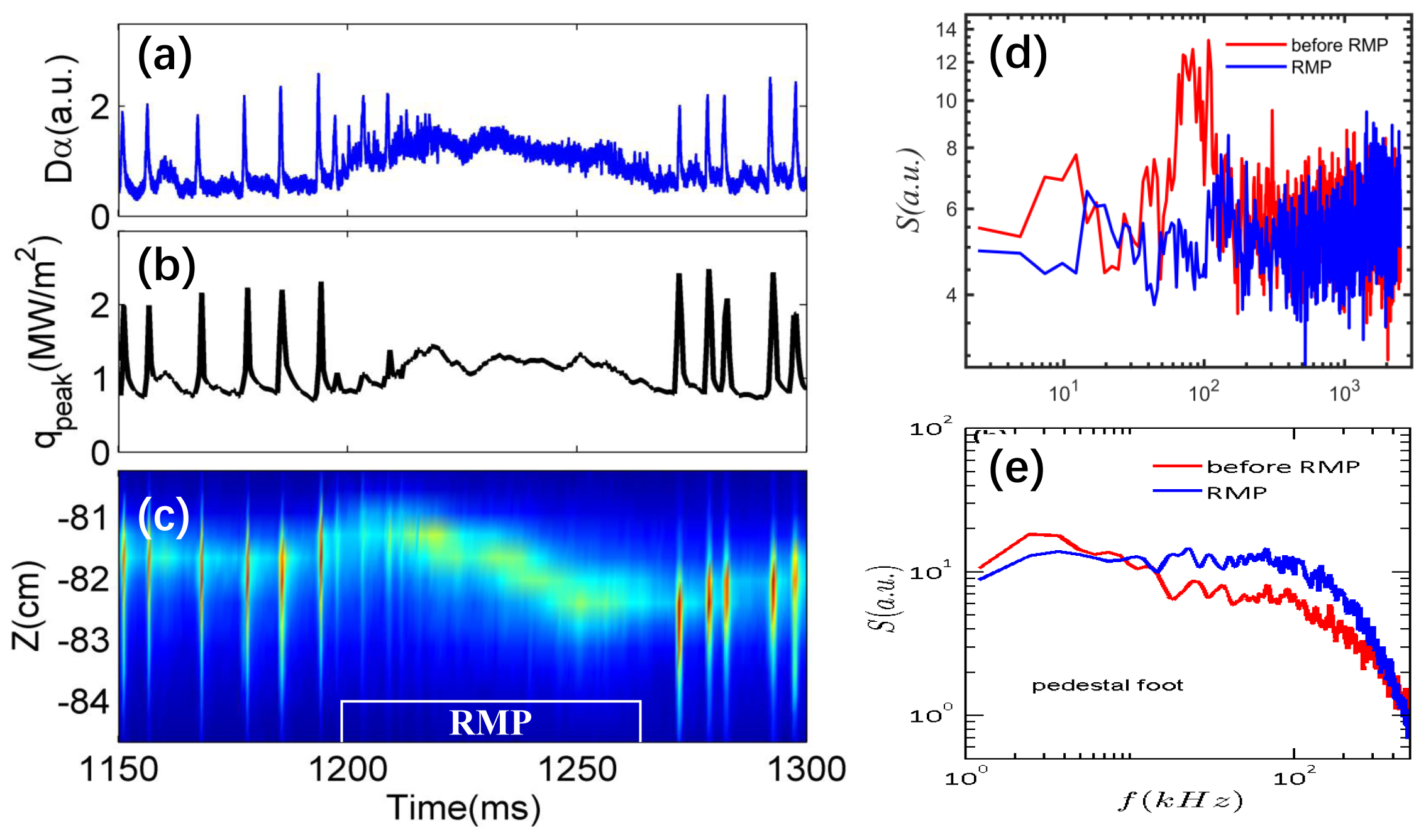 
We mention that suppression of type-I ELMs in HL-2A is globally confirmed across all diagnostics utilized to monitor the ELM properties, including the particle flux to the divertor target plate and heat flux measured by an infrared camera.
To gain deeper insight into the impact of RMP on the plasma edge behavior during ELM suppression, we have investigated the changes in the pedestal height, the plasma rotation, and the turbulence in the pedestal region. The key finding is an observed increase of the turbulence level [Fig.1(e)] at the pedestal foot, which in turn appears to effect a mild decrease in the pedestal height. Further MHD calculations show that the peeling-ballooning modes become stable during the RMP-on phase. Another, and perhaps the most interesting experimental observation, is the significant decrease in the edge poloidal flow measured by a Doppler reflectometry, after application of the RMP. Reduction of edge poloidal flow may be in direct correlation with the enhancement of turbulence in the pedestal foot. We also find that the impulsive transport associated with ELMs is replaced by an increase in the turbulent transport. More detailed study on the flow damping dynamics due to RMP and its role in enhancing the turbulence at the pedestal foot is on-going.
Flow damping has also been observed in the ASDEX Upgrade ELM control experiments. In one set of experiments, it was found that the core plasma toroidal rotation was significantly reduced by the RMP field induced $m/n = 1/1$ plasma response. We carry out both linear and quasi-linear plasma response modelling, assuming the $n=1$ RMP field as in experiments. The computational tools that we utilize are the MARS-F $[4]$ and MARS-Q $[5]$ codes. For the linear plasma response, several aspects are primarily investigated: (i) comparison of the poloidal spectra between the vacuum field and the plasma response fields, (ii) the plasma boundary corrugation due to 3D fields, (iii) comparison of toroidal torques, including the neoclassical toroidal viscous (NTV) torque $[6]$ and torques associated with the Maxwell and Reynolds stresses. For the quasi-linear plasma response, we investigate the (physically) non-linear interaction between the core plasma toroidal flow and the plasma response to the RMP field. The toroidal torques usually act as the sink term in the momentum balance equation, leading to flow damping $[7, 8]$.
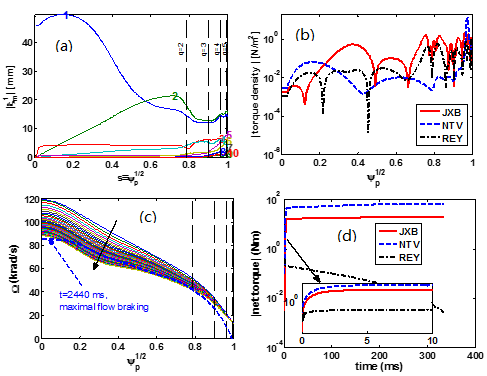
The simulation results are summarized in Figure 2. Linear response computations show a large internal kink response [Fig. 2(a)] when the plasma central safety factor $q_0$ is just above 1. This internal kink response induces neoclassical toroidal viscous (NTV) torque [Fig. 2(b)] in the plasma core, which is significantly enhanced by the precessional drift resonance of thermal particles in the super-banana regime. Quasi-linear simulation results reveal a core plasma flow damping by about $25\%$, agreeing well with experimental observations, with the NTV torque playing the dominant role [Fig. 2(c) and (d)]. Sensitivity studies indicate that the internal kink response and the resulting core flow damping critically depend on the plasma equilibrium pressure, the initial flow speed, the coil phasing and the proximity of $q_0$ to 1. No appreciable flow damping is found for a low $\beta_N$ plasma. A relatively slower initial toroidal flow results in a stronger core flow damping, due to the enhanced NTV torque. Weaker flow damping is achieved as $q_0$ is assumed to be farther away from 1. Finally, a systematic coil phasing scan finds the strongest (weakest) flow damping occurring at the coil phasing of approximately 20 (200) degrees, again quantitatively agreeing with experiments. This study points to the important role played by the internal kink response in plasma core flow damping in high-beta hybrid scenario plasmas such as that foreseen for ITER.
References
$[1]$ A. Loarte et al. Nucl. Fusion 54 033007 (2014)
$[2]$ Evans T.E. et al 2004 Phys. Rev. Lett. 92 235003
$[3]$ Piovesan P. et al 2017 Plasma Phys. Control. Fusion 59 014027
$[4]$ Liu Y.Q. et al 2000 Phys. Plasmas 7 3681
$[5]$ Liu Y.Q. et al 2013 Phys. Plasmas 20 042503
$[6]$ Sun Y. et al 2010 Plasma Phys. Control. Fusion 52 105007
$[7]$ Zhang N. et al 2018 Phys. Plasmas 25 092502
$[8]$ Zhang N. et al 2017 Phys. Plasmas 24 082507
| Affiliation | Southwestern Institute of Physics |
|---|---|
| Country or International Organization | China |
