Speaker
Description
We present a new model of the sawtooth oscillation that can explain direct measurements which show $q_0$ well below 1 during the entire cycle, and observations that indicate the $q=1$ surface is not removed by the sawtooth crash.
In this model the crash is caused by an ideal instability that occurs when $q_0=2/3$.
This instability changes the topology of the nested magnetic surfaces around the axis into that of an alternating-hyperbolic point.
This stochastisizes a region around the axis that resets $q_0$ to a value above $2/3$ but below 1.
Understanding and controlling this internal disruption is important for future tokamaks such as ITER.
The leading sawtooth models are by Kadomtsev (1) and Wesson (2).
Both these models predict that the crash occurs when $q_0\sim1$, through the action of the ideal $1/1$ internal kink mode.
This process removes the $q=1$ surface and resets $q_0$ to 1.
This is confirmed by direct measurements where the reset of the central safety factor is observed (3).
However, the internal kink can be stabilized in many ways (4), and the effects of this stabilization on the $1/1$ sawtooth is seen in experiments (5, 6).
Furthermore, there are several observations that are irreconcilable with the Wesson and Kadomtsev models.
The safety factor was directly measured on TEXTOR using Faraday rotation imaging (7), and on TFTR using MSE (8, 9).
These two different experiments, performed using two different methods, on two different tokamaks gave the same result: The crash occured when $q_0=0.7\pm0.1$, and stayed well below 1 for the entire cycle.
Other measurements indicate that the $q=1$ surface is not always removed: The snakes (10,11) observed on JET, which are associated with islands on the $1/1$ surface, can survive multiple sawtooth crashes.
A close analysis of EAE activity additionally reveals shots where the EAEs associated with the $q=1$ surface are not removed by the sawtooth crash (12).
We show that every configuration of the magnetic field around a closed field line (for example the magnetic axis) corresponds with an element $\mathsf{M}$ of the simple Lie group $\mathrm{SL}(2,\mathbb{R})$, the group of $2\times2$ real valued matrices with unit determinant.
This group contains distinct subsets, classified by their trace, in which the topology of the magnetic surfaces differ.
These subsets comprise the O-points ($|\mathrm{Tr}(\mathsf{M})|<2$), the X-points ($\mathrm{Tr}(\mathsf{M})>+2$), points on an intact $q=1$ surface ($\mathrm{Tr}(\mathsf{M})=+2$), and \emph{alternating-hyperbolic} points ($\mathrm{Tr}(\mathsf{M})<-2$).
An alternating-hyperbolic point is surrounded by hyperbolic surfaces just as an X-point, but the field line map includes reflection in the fixed point.
During a discharge the magnetic field changes continuously, and so does the matrix $\mathsf{M}$ associated with a closed field line.
The matrix $\mathsf{M}$ can transition to a different subgroup of $\mathrm{SL}(2,\mathbb{R})$, where the field changes topology, when $\mathrm{Tr}(\mathsf{M})=\pm2$.
The traditional $1/1$ sawtooth involves such changes at the intact $q=1$ surface where $\mathrm{Tr}(\mathsf{M})=2$, which changes into an X-point and an O-point.
The O-point of the 1/1 island becomes the new axis with $q_0=1$.
A transition of a different nature occurs when $\mathrm{Tr}(\mathsf{M})=-2$, which is the case when $q_0=2/3$.
Here the magnetic axis can change into an alternating-hyperbolic point.
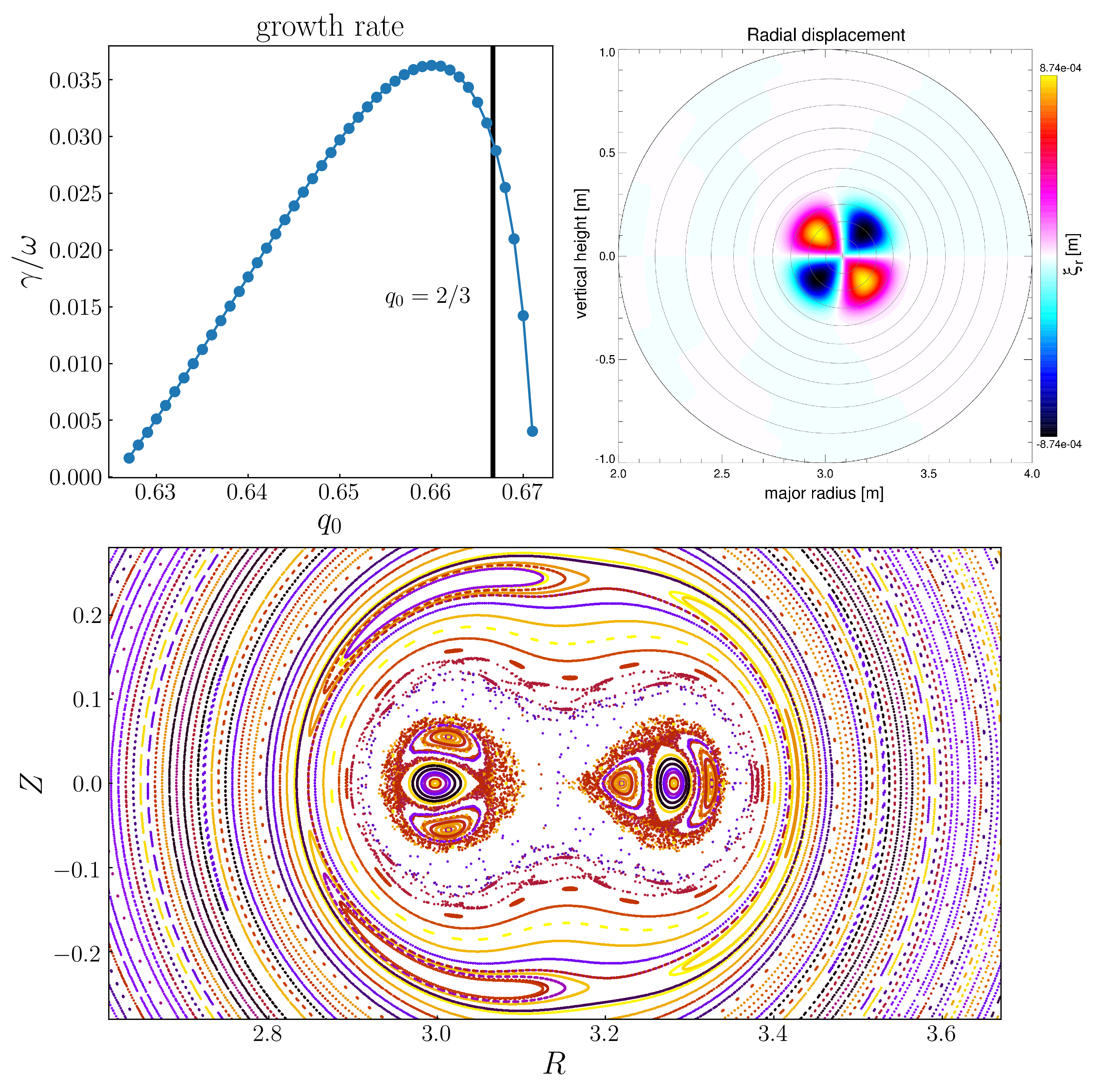
When we investigate the stability of ideal MHD equilibria with $q_0=2/3$ using NOVA-K, we find an ideal $2/3$ mode localized on the axis.
This instability occurs slightly before $q_0$ reaches $2/3$, and has a higher growth rate than the $1/1$ internal kink for similar values of plasma $\beta$.
The growth rate and mode profile are shown in figure 1.
The perturbed field associated with this mode is calculated from $\delta \mathbf{B} = \nabla\times\left(\mathbf{\xi}\times\mathbf{B_0}\right)$.
This perturbation causes an immediate change in topology of the magnetic surfaces around the axis into the alternating-hyperbolic configuration.
At high amplitudes this mode stochastisizes a region around the axis, and breaks the $q=1$ surface into a $3/3$ island chain.
A poincar\'e plot of the stochastisized field is shown in figure 1.
This leads to the alternating-hyperbolic model for the sawtooth:
The internal kink is stabilized until $q_0=2/3$.
The unstable $2/3$ mode is triggered and the axis is changed into an alternating-hyperbolic fixed point, which stochastisizes the core region.
The magnetic connectivity in the stochastic region can then drive rapid reconnection, which would redistribute poloidal and toroidal fluxes and increase $q_0$.
The cycle repeats, until through slow current diffusion $q_0$ reaches $2/3$ again.
This model predicts the crash well within the uncertainty of the measured value of $q=0.7\pm0.1$ (7, 8, 9), it predicts $q_0$ below 1 for the entire cycle, and it does not remove the $q=1$ surface, explaining the persistence of snakes and EAEs.
(1) B. B. Kadomtsev, Soviet Journal of Plasma Physics 1, 710 (1975).
(2) J. A. Wesson, Plasma physics and controlled fusion 28, 243 (1986).
(3) Y. B. Nam, J. S. Ko, G. H. Choe, Y. Bae, M. J. Choi, W. Lee, G. S. Yun, S. Jardin, and H. Park, Nuclear Fusion 58, 066009 (2018).
(4) I. T. Chapman, S. D. Pinches, J. P. Graves, R. J. Akers, L. C. Appel, R. V. Budny, S. Coda, N. J. Conway, M. De Bock, L. G. Eriksson, et al., Plasma Physics and Controlled Fusion 49, B385 (2007).
(5) C. Angioni, A. Pochelon, N. N. Gorelenkov, K. G. McClements, O. Sauter, R. V. Budny, P. C. De Vries, D. F. Howell, M. Mantsinen, M. F. F. Nave, et al., Plasma physics and controlled fusion 44, 205 (2002).
(6) D. J. Campbell, D. F. H. Start, J. A. Wesson, D. V. Bartlett, V. P. Bhatnagar, M. Bures, J. G. Cordey, G. A. Cottrell, P. A. Dupperex, A. W. Edwards, et al., Physical review letters 60, 2148 (1988).
(7) H. Soltwisch and H. Koslowski, Plasma physics and controlled fusion 37, 667 (1995).
(8) F. M. Levinton, S. H. Batha, M. Yamada, and M. Zarnstorff, Physics of Fluids B: Plasma Physics 5, 2554 (1993).
(9) M. Yamada, F. Levinton, N. Pomphrey, R. Budny, J. Manickam, and Y. Nagayama, Physics of plasmas 1, 3269 (1994).
(10) A. Weller, A. D. Cheetham, A. W. Edwards, R. D. Gill, A. Gondhalekar, R. S. Granetz, J. Snipes, and J. A. Wesson, Physical review letters 59, 2303 (1987).
(11) R. D. Gill, A. W. Edwards, D. Pasini, and A. Weller, Nuclear Fusion 32, 723 (1992).
(12) G. J. Kramer, C. Z. Cheng, Y. Kusama, R. Nazikian, S. Takeji, and K. Tobita, Nuclear fusion 41, 1135 (2001).
| Affiliation | Princeton Plasma Physics laboratory |
|---|---|
| Country or International Organization | United States |
