Speaker
Description
New power law scalings of the error field (EF) penetration thresholds across a wide range of tokamaks have been developed for toroidal mode numbers n=1 and 2 and project values for ITER that the construction tolerances and correction coils satisfy. This paper presents a multi-variable n=2 threshold regression across a wide range of densities, toroidal fields, and pressures in 3 machines (DIII-D, EAST, and COMPASS) using a common metric to quantify the EF in each device. It compares this new n=2 scaling to updated n=1 scalings using a larger 6 machine ITPA database. The results validate nonlinear single-fluid MHD simulation scalings, which are used to lend confidence to the projected scalings to ITER. These projections set the tolerances for non-axisymmetric components (like Test Blanket Modules) and the corresponding requirements for EF correction coil arrays in ITER.

Nonaxisymmetric fields four orders of magnitude smaller than the axisymmetric field can drive islands that cause disruptions in tokamaks; and the GPEC overlap metric, $\delta$, provides a way of identifying and quantifying the most dangerous of these asymmetries. The metric uses a resonant field spectrum determined from a combination of the applied field and the plasma response (amplification and/or shielding of various components)$^{1, 2}$, surpassing the robustness of the old “3-mode” vacuum model$^{3}$. Tolerances for the design and optimization of tokamak coils have been projected to ITER using fit scalings of this overlap metric with macroscopic 0D parameters that are easily identified both in current and for future devices.
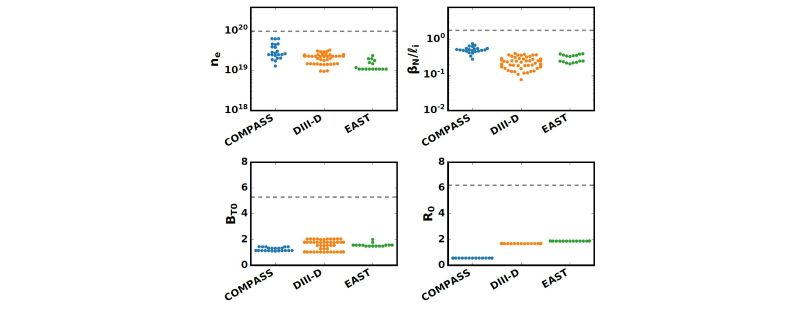
The n=2 database, consisting of 3 devices and a parameter range shown in Figure 1, reveals tolerances of a similar order of magnitude to those for n=1 in current devices. Experimental thresholds are determined by ramping up artificial EFs using 3D field coil arrays until a core island penetration event is observed and recording the corresponding amplitude in EF overlap $\delta$. The predictions of a power law fit to this data using a kernel density weighted regression are compared to the true experimental thresholds in Figure 2. The full regression used has a density scaling exponent of 1.07±0.09, a toroidal field exponent of -1.52±0.2, a major radius exponent of 1.46±0.09 and a normalized pressure ($\beta_N/\ell_i$) exponent of 0.36±0.11. This fit projects very high n=2 thresholds for ITER due to the strong size scaling.
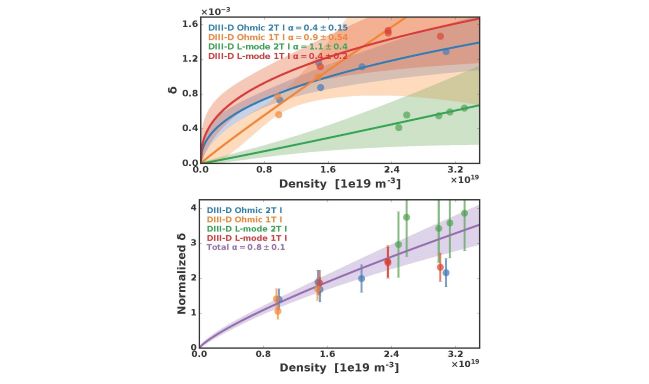
Although single parameter scans across regimes accessible by a single machine can reveal varied behaviors, the multi-variable, multi-machine scaling provides the most robust projection to new devices. Figure 3 shows individual density scans in DIII-D can exhibit a wide variety of trends depending on the initial target plasma. The second panel, however, shows how the seemingly discrepant DIII-D experiments are unified when normalizing by the general toroidal field and pressure scalings. Observations at even higher density show that ohmic confinement regime transitions in any given device can drastically alter the density scaling in that particular experiment. The ratio of non-resonant to resonant 3D field applied in a given experiment also alters the dynamics through neoclassical toroidal viscosity (NTV) braking. Recent advances in optimization of nonresonant fields for robust quasi-symmetry minimizing such secondary effects are beyond the scope of this dominant-order resonant field analysis. The local and secondary phenomena are purposely smoothed out in the multi-machine scaling presented here, in an intentionally analogous manner to the treatment of single-machine variations in the international confinement scalings that have proven so useful for the fusion community.
The nonlinear, single fluid MHD code TM1 has been used to model the experimental scalings, providing confidence in some scalings and insight into experimental needs. The model reproduces the experimentally observed toroidal field and $\beta_N/\ell_i$ scaling, and shows the scalings hold out to ITER values. The density scaling exponent calculated by TM1 falls below the experimental n=2 fit, closer to the better constrained n=1 empirical fit. This, and a large discrepancy between n=1 and 2 size scalings, identifies what n=2 data is needed to improve ITER projections. The code projects n=2 thresholds in ITER roughly 2-3 times that of the projected n=1 thresholds, consistent with observations in existing devices to date.
This combination of robust, cross-regime experimental scalings and tightly coupled modeling project EF tolerances of above a Gauss for both n=1 and 2 EFs in ITER, which are criteria the ITER construction tolerances and correction coils easily satisfy.
This work was supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, using the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Awards DE-AC02-09CH11466 and DE-FC02-04ER54698.
- J.-K. Park, A.H. Boozer, et. al, Physics of Plasmas 16, 056115 (2009).
- N.C. Logan, C. Paz-Soldan, et. al, Physics of Plasmas 23, 056110 (2016).
- J.-K. Park, N. C. Logan, et. al, ITPA MHD, ITER Report #ITER_D_UMLSUW (2017).
| Affiliation | Princeton Plasma Physics Laboratory |
|---|---|
| Country or International Organization | United States |
