Speaker
Description
Full suppression of Edge Localized Modes (ELMs) by using n=4 resonant magnetic perturbations (RMPs) has been demonstrated for ITER for the first time (n is the toroidal mode number of the applied RMP). This is achieved in EAST plasmas with low input torque and tungsten divertor, thus also addressing significant scenario issues for ITER. In these conditions energy confinement does not drop significantly (<10%) when ELM suppression is achieved compared to the ELMy H-mode conditions, while core plasma tungsten concentration is clearly reduced. The target plasma for these experiments in EAST is chosen as close as possible to the ITER type-I ELMy H-mode operational scenario with low torque input. In these experiments the NBI torque is around $T_{\mathrm{NBI}}$ ~ 0.3-0.4Nm, which extrapolates to 11 – 16 Nm in ITER (compared to a total torque input of 35 Nm when 33 MW of NBI are used for heating). The observed ELM suppression window is consistent with the peak in the modeled edge stochasticity using the MARS-F code. ELM suppression is maintained up to 60% $N_{\mathrm{GW}}$ (the Greenwald density) by feedforward gas fueling after suppression is achieved. These results expand physical understanding and demonstrate the potential effectiveness of RMP for reliably controlling ELMs in future ITER high Q plasma scenarios.
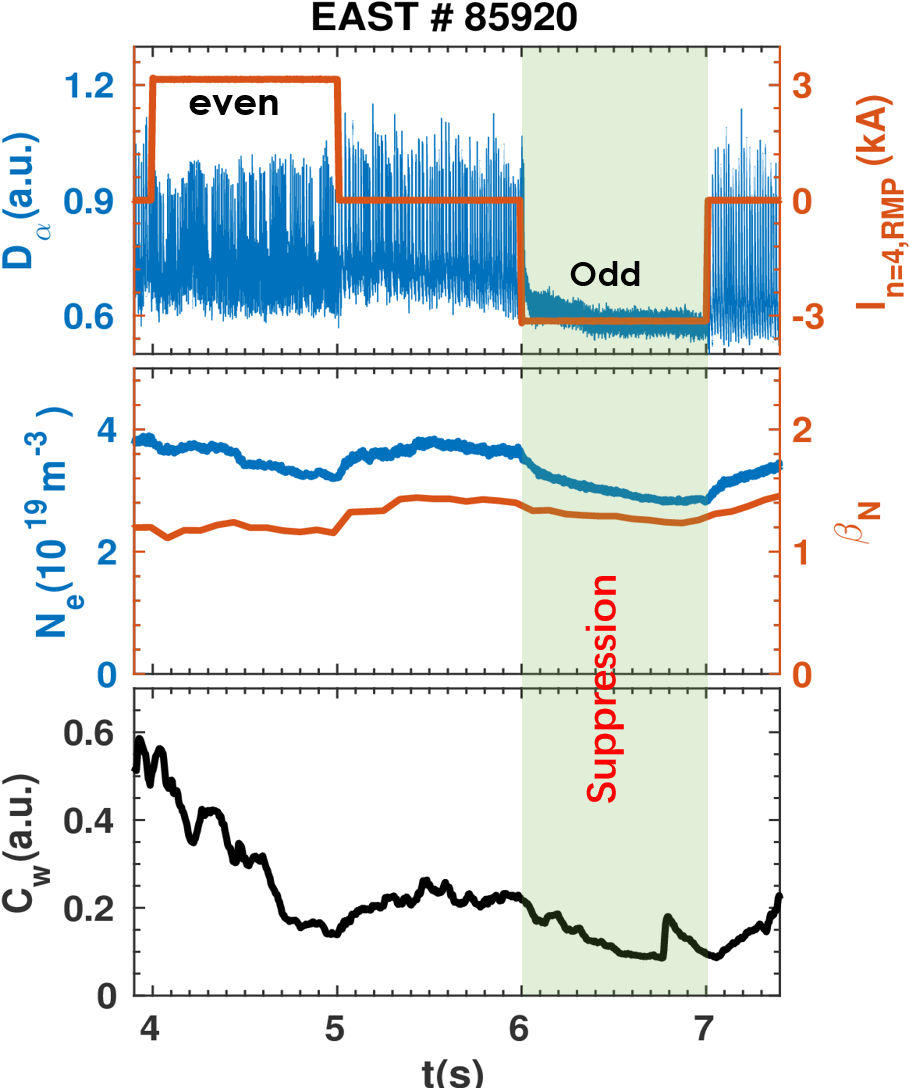
Plasma energy confinement during ELM suppression in these EAST plasmas decrease very slightly (< 10%) compared to the Type I ELMy H-mode with no RMPs applied, as shown in Fig. 1. This is very different from previous observations using low n (n=1 and 2) RMPs in EAST with high $q_{95}$ (≥4) [Ref.1]. As shown in Fig. 1, ELMs are completely suppressed by using n =4 RMPs with odd parity (opposite phases in the upper and lower rows of coils current) in EAST but not when even parity is applied to a type-I ELMy H-mode plasma with $q_{95}$ ≈3.65 and low input torque (TNBI ~ 0.3-0.4Nm) leading to a plasma beta $\beta_N$ ~ 1.5-1.8, similar to that in the ITER Q =10 scenario. The electron and ion temperature are very similar with $T_{i0}$ ≈ $T_{e0}$ ≈2keV. Significant density pump out (20% reduction) takes place during ELM suppression, while the drop of stored energy is negligible (5%). The tungsten concentration (lower subgraph) is also reduced by a factor of 2 compared to type I ELMy H-mode when ELMN suppression is achieved, despite the lower plasma density. The threshold n=4 RMP current for full ELM suppression is around 2kA (⨉ four turns). Striations of the heat and particle fluxes at the divertor target are observed during ELM suppression and are consistent with the modeled magnetic footprint by TOP2D.
Suppression windows in both $q_{95}$ and plasma density are observed; in addition, lower plasma rotation favours access to ELM suppression. ELM suppression is achieved in a narrow $q_{95}$ window in [3.6, 3.8] with odd n=4 RMP configuration with a continuous q95 ($I_p$ ramp-up). ELM suppression can be maintained up to 60% of Greenwald density by feedforward gas fueling after suppression. It is interesting to note that there is not only an upper density but also a lower density threshold for ELM suppression of 40% $N_{\mathrm{GW}}$. Outside the $q_{95}$ and density window only ELM mitigation, not suppression, is observed.
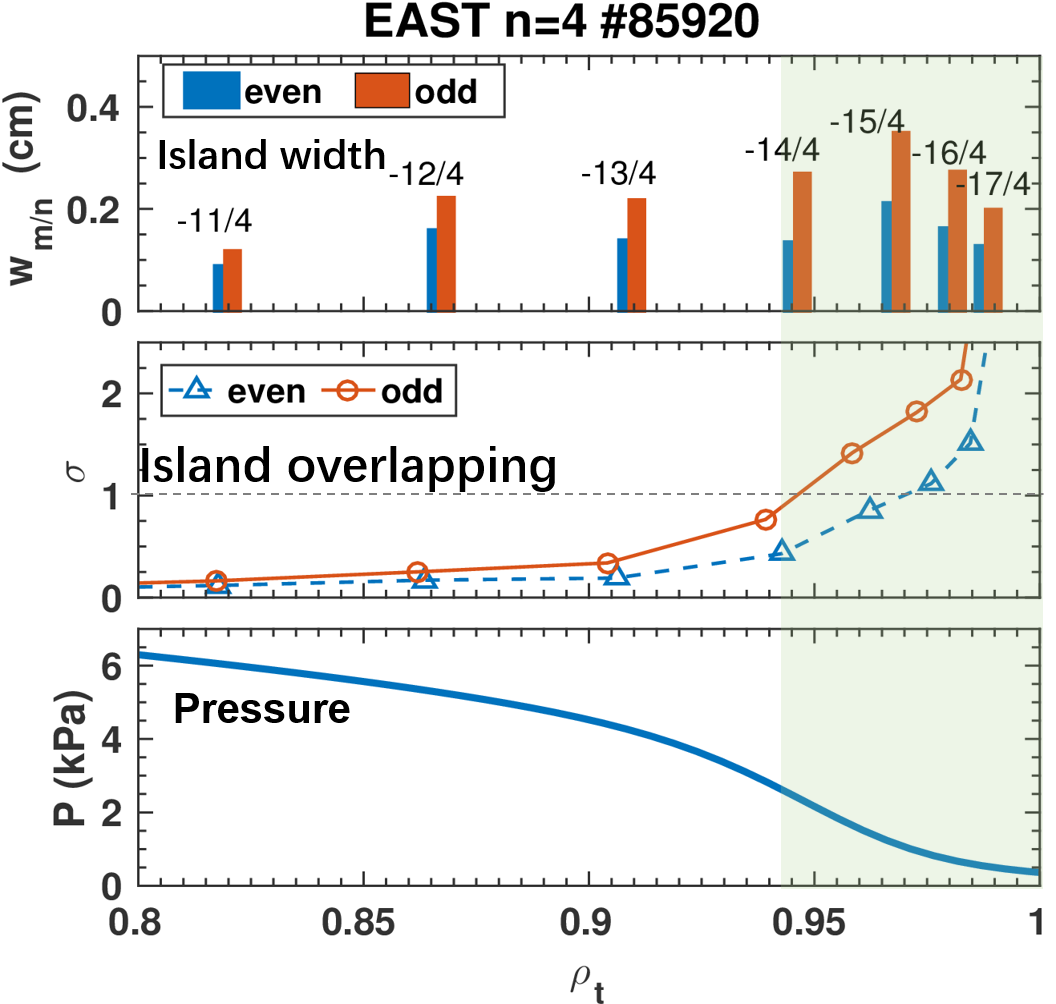
The modelled magnitude of edge stochasticity taking into account the linear MHD plasma response evaluated with MARS-F [Ref.2] is found to be strongly linked to the observed ELM suppression effect. Although vacuum modeling by the MAPS code shows that the edge resonant harmonics are stronger for the even coil configuration, MARS-F shows that the plasma shielding effect is stronger for the even coil configuration than for the odd one. The edge resonances with plasma response shown in Fig. 2 are stronger for the odd coil configuration; this applies not only the resonant harmonic just near the pedestal top (m = -13, n =4) but to the other edge resonant harmonics as shown in Fig. 2. Therefore, the edge stochasticity, i.e. edge Chirikov parameter ($\sigma$) or stochastic layer width ($\delta_{\mathrm{ergodic}}$) might be a better figure of merit for ELM control optimization (previous studies for this parameter [Ref. 3] did not account for plasma response). Including plasma response leads to edge magnetic field stochasticity for odd parity configuration being higher than that for the even one, which is consistent with the experimental results in Fig. 1.
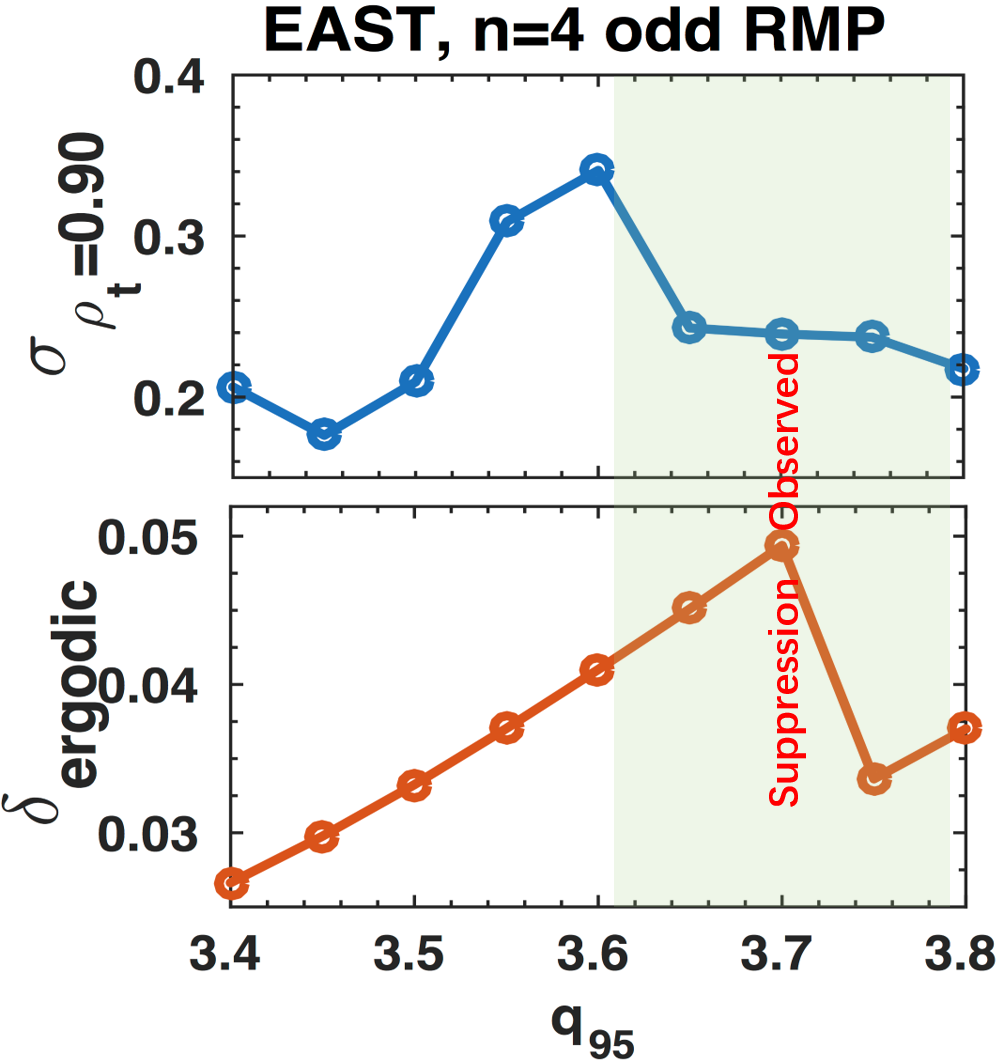
The observed ELM suppression window in this experiment provides a good opportunity to test the effectiveness of different figure of merits for ELM control optimization. MARS-F modelling shows that both the Chirikov parameter near the pedestal top and the normalized edge stochastic layer width have a peak at $q_{95}$~3.6-3.7 for the odd parity configuration as shown in Fig. 3. The resonant window modeled by $\delta_{\mathrm{ergodic}}$ agrees well with the suppression window observed in this experiment. Comparison between different criteria including pedestal top island width and edge X-point displacement to this experimental observation will also be presented. Further detailed modelling studies and experimental analysis of the 3D physics processes in these experiments will be addressed in this presentation, with the objective to expand physics understanding for ELM suppression and to provide a solid physics basis for its extrapolation to future burning plasma devices such as ITER.
This work is supported by the National Key R&D Program of China under Grant No. 2017YFE0301100, the National Natural Science Foundation of China under Grant No. 11875292 and U.S. DOE under DE-SC0020298.
References:
(1) Sun Y et al, Phys. Rev. Lett. 117, 115001 (2016).
(2) Liu Y et al, Phys. Plasmas 17, 122502 (2010).
(3) Evans T et al, Phys. Rev. Lett. 92, 235003 (2004).
| Affiliation | Institute of Plasma Physics, Chinese Academy of Sciences |
|---|---|
| Country or International Organization | China |
