Speaker
Description
The role of the nonadiabatic electron drive in regulating the isotope mass scaling of gyrokinetic turbulence is assessed in the transition from ion-dominated core transport regimes to electron-dominated edge transport regimes. The scaling of the plasma energy confinement time with hydrogenic isotope mass is of critical importance, as most tokamaks operate with deuterium (D) as the main ion species, while ITER calls for dominant hydrogen (H) operation in the first phase, transitioning to 50:50 deuterium-tritium (DT) fuel composition at reactor-level operation. Experimental observations often show confinement improving with increasing ion mass {1}. Simple gyroBohm-scaling theoretical arguments (that ignore electron dynamics), however, predict that the turbulent ion energy flux scales with the square root of the ion mass, with the implication that the global confinement degrades with increasing ion mass. Using nonlinear gyrokinetic simulations of DIII-D, we illustrate a remarkable transition in the turbulent isotope scaling towards the plasma L-mode edge. The transition is controlled by finite electron-to-ion mass-ratio dependence of the nonadiabatic electron response, dominantly generated by the parallel motion, which represents a correction to bounce-averaging of the electrons. The nonadiabatic electron drive strongly regulates the turbulence levels and plays a key role in altering -- and in the case of the DIII-D edge, reversing -- the simple gyroBohm scaling rule. The finite electron-mass correction is larger for light ions and increases with increasing $q$ so that, while it is weak in the core, it dominates the mass scaling in the edge. Overall, these results may have favorable implications for global energy confinement and for the power threshold for the L-mode to H-mode transition in a reactor like ITER from H to D to DT, consistent with recent experimental observations comparing hydrogen and deuterium plasmas {2}.
Theoretical basis for gyrokinetic isotope scaling
The ion gyrokinetic equation together with the assumption of purely adiabatic electrons describes ion energy fluxes $Q_a$ that exhibit simple gyroBohm scaling:
$\qquad Q_a = C_0 \, Q_{\rm GBa} \quad\text{where}\quad Q_{\rm GBa} = Q_{\rm GBD} \sqrt{m_a/m_{\rm D}} \; .$
Here, the subscript $a$ is the species index, $Q_{\rm GBD} \doteq n_e T_e c_{sD} \rho_{*D}^2$ is the deuterium gyroBohm energy flux, $c_{sD}=\sqrt{T_e/m_D}$ is the deuterium sound speed and $\rho_{*D}=(c_{sD}/\Omega_{D,{\rm unit}})/ a$ is the normalized deuterium ion-sound gyroradius. Because $C_0$ is species-independent, we must always observe $Q_{\rm H} < Q_{\rm D} < Q_{\rm T}$, i.e. heavier isotopes should give rise to confinement degradation. When kinetic electron dynamics are fully retained, however, we expect the more complicated true gyroBohm scaling:
$\qquad Q_a = C\left(m_e/m_a\right) Q_{GBa} \; ,$
that contains an additional electron-to-ion mass-ratio dependence. We observe that the $m_e/m_a$ mass dependence of $C$ typically opposes the simple gyroBohm mass dependence, and can in some cases dominate and reverse the gyroBohm dependence so that $Q_{\rm H} > Q_{\rm D} > Q_{\rm T}$.
Reversal of simple gyroBohm scaling in electron-transport dominated edge regimes
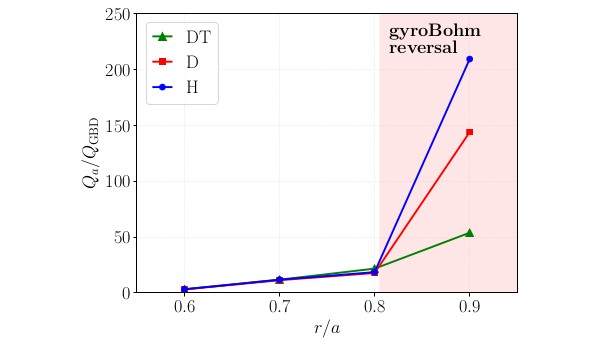
Using CGYRO {3} we gauge the influence of kinetic electrons on the isotope scaling of energy flux in the transition from ion-dominated (core) transport regimes to electron-dominated (edge-typical) transport regimes. Simulation parameters are based on DIII-D #173147 at t=1705ms, an ohmically-heated L-mode discharge. Fig. 1 shows that CGYRO matches the total (e+i) experimental power-balance flux in both the ion-dominated core and the electron-dominated edge ($r/a \ge 0.9$), where $Q_e \sim 1.5 \, Q_i$ and TGLF underestimates the edge electron transport. The dominant linear mode in the core is ion-temperature-gradient (ITG) driven, whereas in the edge an electron temperature gradient-driven trapped electron mode (TEM) dominates. Fig. 2 compares the simulated ion energy flux for deuterium versus hydrogen versus 50:50 DT as the main ion species (with all other experimental parameters fixed). In the ITG-dominated regime, $Q_{\rm H} \sim Q_{\rm D} \sim Q_{\rm DT}$, meaning simple gyroBohm scaling is broken. This is dominantly due to electron collisions, which more strongly stabilize heavier species {4}, and weakly to the ${\mathbf E} \times {\mathbf B}$ flow shear {5}. However, a near gyroBohm scaling can be recovered by scaling the electron collision rate and the ${\mathbf E} \times {\mathbf B}$ shearing rate with the main ion thermal speed. In contrast, in the TEM-dominated edge regime, a strong reversal from the gyroBohm scaling is found, with $Q_{\rm H} \gg Q_{\rm D} \gg Q_{\rm DT}$. This implies that hydrogen confinement relative to deuterium is expected to be significantly worse than expected by the simple gyroBohm mass scaling. We demonstrate that this reversal is due to the nonadiabatic electron drive from the kinetic electron parallel response which acts to enhance the TEM turbulence for light ions.

Key role of the nonadiabatic electron response
The reversal from gyroBohm scaling in the electron transport-dominated edge is controlled by finite electron-to-ion mass-ratio dependence of the nonadiabatic electron response {6}. At fixed plasma gradients, this nonadiabatic effect is strongly enhanced at increased $q$, as shown in Fig. 3, and thus dominates in the plasma edge. This is consistent with the $q$-dependence of the electron parallel timescale relative to the ion drift timescale: $({\rm v}_i/a) \tau_e \sim q (R_0/a) {\rm v}_i/{\rm v}_e \sim q (R_0/a) \sqrt{m_e/m_i}$. For massless electrons, $\tau_e \rightarrow 0$, such that the passing nonadiabatic distribution vanishes and the trapped distribution is bounce-averaged and independent of mass ratio. At finite electron mass, the nonadiabatic correction increases with $q$ and decreases with $m_i$. Thus, for light species like hydrogen, deviation from the bounce-averaged limit is larger than for deuterium. Electron collisions provide a secondary mass-ratio correction to the flux scaling, so to recover simple gyroBohm scaling at low $q$ it is also necessary to reduce the collision frequency to eliminate $m_e$-dependence of the trapped-passing boundary layer width (shown in Fig. 3 for $q<2$ when ${\bar \nu}_e \rightarrow 0$).

Implications for global confinement and the L-H threshold in a reactor
For assessing the isotope scaling of global energy confinement in a reactor like ITER, it is essential to properly treat the precise nonadiabatic electron dynamics. Fluid or even bounce-averaged electron models are unlikely to recover the correct ion-mass scaling. For a full transport analysis, additional influences (e.g. impurities, heating, MHD) beyond the scope of this work must also be considered. However, plasma confinement is known to be sensitive to edge conditions. Tokamak L-mode edge conditions typically lead to electron transport-dominated turbulence regimes such as studied here, for which the nonadiabatic electron drive is enhanced, resulting in a favorable reversal of the simple gyroBohm scaling with ion mass from H to D to DT. This has implications for lowering the power threshold for the L-mode to H-mode transition in a reactor like ITER and could trend the theoretical turbulent-based global energy confinement isotope scaling toward agreement with experimental observations.
This work was funded by US DOE Grants DE-FG02-95ER54309 and DE-FC02-06ER54873.
{1} ITER Physics Basis Editors, Nucl. Fusion 39, 2175 (1999).
{2} C.F. Maggi et al., Plasma Phys. Control. Fusion 60, 014045 (2018).
{3} M. Nakata et al., Phys. Rev. Lett. 118, 165002 (2017).
{4} J. Garcia et al., Nucl. Fusion 57, 014007 (2017).
{5} J. Candy, E.A. Belli, and R. Bravenec, J. Comput. Phys. 324, 73 (2016).
{6} E.A. Belli, J. Candy, and R.E. Waltz, Phys. Plasmas 26, 082305 (2019).
| Affiliation | General Atomics |
|---|---|
| Country or International Organization | United States |
