Speaker
Description
Mitigation and control of runaway electrons assume greater significance in modern fusion devices because they are acknowledged, as potential threat to in-vesssel components and source for induced instabilities. Their self-mitigation is possible mainly by the loss of energy due to frictional collisions, radiations and collisionless destabilization of various plasma modes. Several other techniques are in use for runaway mitigation viz., low loop voltage startup, enhanced magnetic field, and preferential high Z impurity injection etc. but this still remains a serious threat. The recent observations in DIII-D have established a direct correlation between the destabilization of whistlers and runaway generation, suggesting strongly that the whistlers are driven by the energetic electrons. The necessary condition for the destabilization however suggests that in devices like JET and ITER, the upper hybrid mode may be rather stable, but the whistlers mode may not be. An understanding of whistlers in runaway control and mitigation in a fusion device thus becomes a necessity. Whistlers are excitable by energetic electrons, spatial gradients, beams, loss cones, magnetic mirrors, electron temperature anisotropy, etc. Beside this, whistlers can also be launched actively in plasmas. They induce substantial pitch angle scattering to the energetic electrons and due to their dispersive nature, can result in wave-particle resonance. Higher the whistler activity, the more is the probability of high energy electron scattering, and vice-versa. The whistler based mechanism may prove to be advantageous as runaway scattering might prevent acceleration of electrons to undesirable higher energy. An emphasized role of whistlers requires greater attention, in terms of its underlying physics but its direct investigation is tedious due to complexies involved in tokamaks.
Further, tokamaks offer limited control over the parameters that govern the runaways. Basic plasma devices on the other hand, provide a simplified geometry, a good realization of instabilities and control of some experimental parameters because they are operated at lower plasma density and controllable magnetic field. Thus, there is a clear incentive to study energetic electrons mitigation in basic plasma devices such as large volume plasma device (LVPD) [1]. Despite having differences in geometry and nature of plasmas, it is interesting to note that in LVPD and DIII-D plasmas, the product of normalized growth rate to normalized beam energy (γ_i/ω_ce ×E_b/T_e) maintains same order. Also, both configurations offer boundary free condition to the observed mode. In this paper, we report perhaps first laboratory observation on energetic electrons mitigation in the source plasma of LVPD, abundant with non-thermal electrons. We observed a weaker temperature dependence of growth, in comparison to the tokamak regime, governing destabilization in LVPD where the faster electrons emnates from a loss cone with energy limited to few eV.
We present observations and analysis of whistler destabilization by energetic electrons in LVPD. A pulsed argon plasma is produced (V_d=70V,I_d∼200A,fill pressure of of4×〖10〗^(-4) mbar, n_0∼3×〖10〗^11 cm^(-3)) with Δt_disc∼9.2 ms. The source consists of a bulk population of high-density Maxwellian electrons (T_e∼3eV ) and energetic electrons with energy . Observations showed that turbulence is broadband in nature with significant power residing between 30kHz<ω<80kHz. The observed mode is right hand circularly polarized, indicating that the basic instability driving the turbulence is associated with the whistler mode.
Further, we investigated k_∥ & k_⊥ which are otherwise difficult to measure in tokamaks and thus limits interpretation. As reported[1], growth of the whistler mode and the propagation phase angle are correlated and can be resolved with accurate k_⊥ measurements [Fig.1]. In partially magnetized plasma of LVPD, whistlers are driven by the energetic, reflected electrons from the loss cone. An inverse dependency is observed between the growth of whistlers and energy of streaming electrons. Controlled experiments on their mutual interactions are carried out by electron energy variation through discharge potential (V_d ). The wavenumber (k_∥ & k_⊥) frequency (ω) spectrum is obtained to understand the growth of whistlers. The theoretical basis is derived from the work of Sharma et al. Necessary modifications in the wave propagation direction (k.B≈kB Cosθ) have been incorporated and a close agreement is observed with experiments.
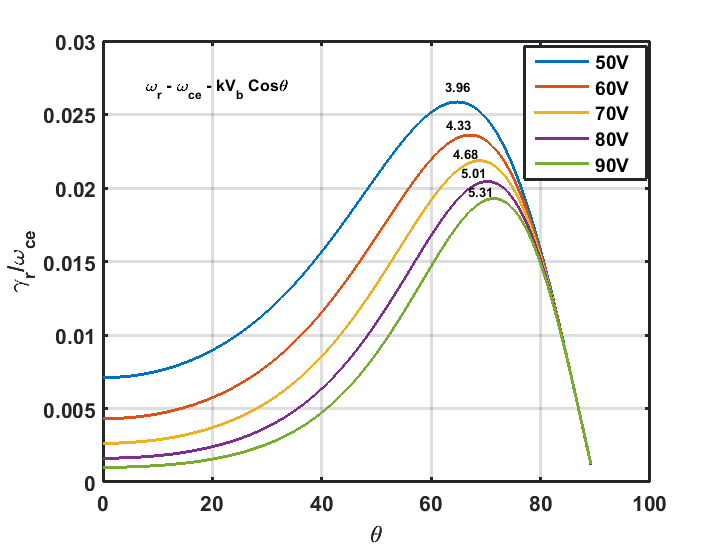
These observations are being correlated with the scattering of the magneto-sonic whistler waves in tokamaks and vice-versa, similar to the theoretical work by Fulop et al., where they estimated the growth when they are destabilized by runaways. We computed growth of whistler mode in LVPD by considering the distribution as Maxwellian for reflected particles, f_r (v_∥,v_⊥ )=n_r 〖f_r〗⊥ (v⊥ ) 〖f_r〗∥ (v∥ ), following the work of Sharma et al. [2]. The plasma dispersion includes contribution of both background plasma (D_r) and reflected particles (D_i), i.e. D_r+〖iD〗i=0. Similarly, Fulop et al. have computed dispersion of runaway electrons by considering Gaussian distribution, implying kinetic theory, it becomes, f(v∥,v_⊥,t)=F(p_∥,t)g(v_∥,v_⊥ ). The runaways are characterised as a beam with parallel momentum greater than perpendicular momentum (m_r v_∥ >>m_r v_⊥). In LVPD, similar situation exists as energetic electrons are treated as beam electrons within the background plasma (v_∥≫v_⊥). The frequency ordering in both cases remains〖 ω〗_ci<ω_0≪ω_ce. First order perturbation analysis shows that whistler growth has direct proportionality with runaway density (γ_i α ω_pr^2), similar to LVPD where it is proportional to the reflected particle density (γ_i α n_r). The growth rate dependency on electron temperature is also explored for the two plasmas. We found that the growth rate of whistlers for DIII-D tokamak(γ_i α 1/(T_e^1.5 ) ) and LVPD (γ_i α 1/(T_e^0.5 ) )exhibits inverse relationship with background electron temperature and they differs by for typical plasma density and magnetic field [Fig.2].
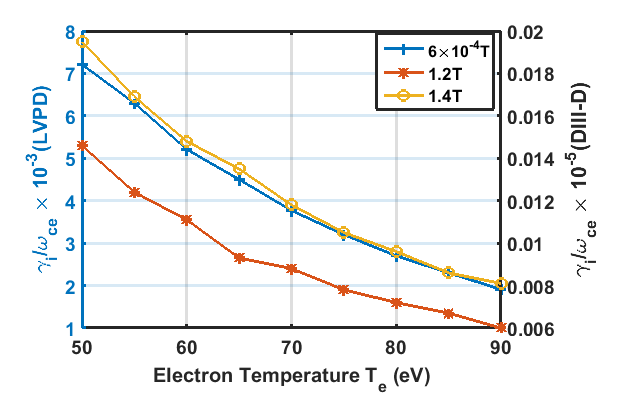
The damping mechanism for tokamaks is electron- ion collisions (γ_d∼1.5τ_ei) and the threshold estimated is, n_re/n_0 =(Z^2 B_T)/(20T_e^1.5 ), originates from the inequality γ_i>γ_d, where, Z is the charge state, B_T is the toroidal magnetic field, n_re is density of the runaway electrons and n_0 is the plasma density. In collisionless plasma of LVPD, we considered whistlers resonate with cyclotron motion of electrons and computed the growth for the mode using inequality (γ_i>γ_d) by considering the cyclotron damping. We obtained the relationship is, n_r/n_0 >Κ/4 n_0/(B_0 T_eb^0.5 ) where B_0 is the background axial magnetic field, Κ is a constant and T_ebis the energetic electron temperature. Thus, based on these observations, we envisage that LVPD outcome can have parallels with the physics of the interaction between whistlers and the runaways in fusion devices.
References:
[1] A. K. Sanyasi, L. M. Awasthi, P. K. Srivastava, S. K. Mattoo, D. Sharma, R. Singh, R. Paikaray, and P. K. Kaw, Phys. Plasmas 24, 102118 (2017).
[2] R. R. Sharma and Loukas Vlahos, The Astrophysical Journal 280, 405(1984).
[3] T. Fulop et al., Phys. Plasmas 13, 062506 (2006).
[4] D. A. Spong et al., Phy. Rev. Lett. 120, 155002 (2018)
[5] Z. Guo, Phys. Plasmas 25, 032504 (2018).
| Affiliation | Institute for Plasma Research, Bhat, Gandhinagar - 382428, India |
|---|---|
| Country or International Organization | India |
