Speaker
Description
Accurate equilibrium reconstruction is crucial for the operation of MAST-U, as well as for stability analyses and disruption event characterization and forecasting. A neural network trained on ideal MHD stability calculations performed on NSTX data accurately predicts the no-wall stability limit for MAST. Stability calculations in projected high beta MAST-U equilibria show a gap between the no-wall and with-wall beta limits due to eddy currents driven in newly installed conducting divertor plates, opening a region of high beta operating space for potentially stable operation if the resistive wall mode is stabilized by non-ideal effects.
Equilibrium Reconstruction- Three different levels of equilibrium reconstruction are tested for MAST plasmas, first with magnetics data only. The second level, called “kinetic”, also includes partial pressure profile constraints from electron pressure from Thomson scattering and ion temperature from charge exchange recombination spectroscopy. Finally, magnetic pitch angle data from motional Stark effect diagnostic (MSE) is added to the kinetic reconstruction. The equilibrium reconstructions also include fitting of field shaping coil currents, and for equilibrium analyses of spherical tori it is important to include currents in the conducting structure of the tokamak modeled, as they can comprise a significant component of the plasma current well into the plasma current, $I_p$, flat-top. To create the best 2D model of the effective resistances of the wall segments for equilibrium reconstruction, we have created a 3D model of the MAST wall (including 3D features such as NBI ports and other large vessel penetrations, coil casings with 3D flanges, etc.) using the VALEN code and have generated a set of 2D effective resistances of wall segments from the full 3D model. VALEN prediction for the coil case currents match Rogowski coil measurements from MAST operations quite well, giving confidence in the VALEN analysis. This technique is then used to determine effective resistances and estimated currents in vessel segments which are not measured. While the different levels of reconstruction are being continually refined, the magnetic and kinetic reconstructions already show good agreement with measured profiles, including with magnetic pitch angle measurements, even before they are included in the reconstructions.
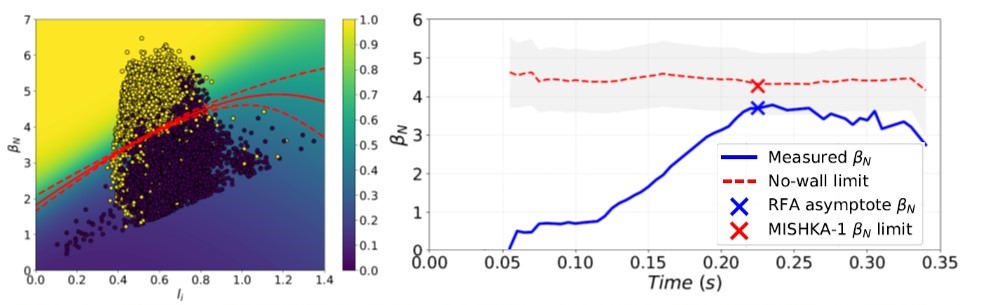
Machine Learning Approaches to Stability – Artificial intelligence and physics knowledge can cooperate in order to build robust real-time disruption avoidance systems (1). Stability physics models in the Disruption Event Characterization and Forecasting code (DECAF) (2) have been updated with two different machine learning algorithms to classify the output of the DCON stability code into stable and unstable regions, for a set of calculations for NSTX. A partially interpretable random forest regressor (RFR) confirmed the most important parameters for ideal stability to be normalized beta, internal inductance, pressure peaking, and aspect ratio. A fully-connected neural network then gave improved closed form equations of the no-wall limit as a function of these parameters. The estimated value of the no-wall limit has been incorporated into the DECAF kinetic stability model. Future high-powered fusion devices, such as ITER, will necessarily be operated in a much more disruption-averse manner than present devices. If machine learning algorithms for disruption avoidance are to help, they must demonstrate that they can be trained on one device and reliably operated on another. Here, our goal is to utilize the training of the ideal stability model on NSTX data and apply it to MAST, to discover the advantages and limitations of such an approach. Figure 1 shows an example of the NSTX-trained $\beta_N$ no-wall formula used on a MAST discharge, for which we can see that the predicted $\beta_N$ no-wall is very close to the MISHKA-1 predictions. It is worth noting that the operating point of these MAST discharges can be somewhat above the domain of applicability of the neural network results. Therefore, the NSTX-trained formula applied to MAST has been influenced by physics guidance that has been applied outside the training region, improving the MAST no-wall limit predictions, as otherwise they would have been larger. This example demonstrates the significant advantage of using multiple machines to validate a machine learning assisted physics model, as doing so can expand the domain of applicability. This might be the necessary path for future devices such as ITER where a small amount of initial data might be used to update algorithms previously trained on full databases of previous machines.
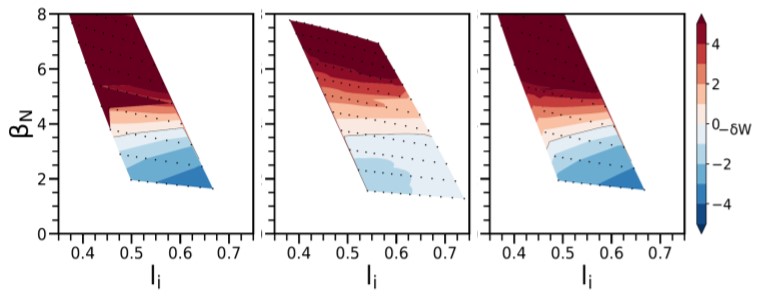
Projections of MAST-U Stability Limits - Projected equilibria have been generated for MAST-U to prepare for operation. These equilibria were assessed with the DCON and MARS-F ideal stability codes to find the no-wall beta limit, and for the “with-wall” limit, theoretically the highest achievable performance point, again with the MARS-F code, including an approximate axisymmetric wall, and with the VALEN code which includes a 3D model of the surrounding conducting structure. The no-wall limit was generally found to increase as plasma internal inductance increased, see Fig. 2. Similar with-wall limits were found, despite the difference between the codes in the treatment of the wall. A gap between the approximate no-wall limits of $\beta_N/l_i$ = 6.44 and 7.13, found from DCON and MARS-F respectively, and the with-wall limits of $\beta_N/l_i$ = 8.68 and 8.53 from VALEN and MARS-F respectively exists due to the increased stabilizing effect of conducting divertor plates, which were newly installed in MAST-U, and are in a region of significant mode perturbation, so eddy currents are driven in these structures. The increased operating space between the no-wall and with-wall beta limits should enable high beta operation in MAST-U. By the present ideal stability analysis, resistive wall modes should be unstable in that operating gap, however various other methods of passive and active stabilization of the RWM has been demonstrated over the years which allows tokamak operation above the ideal no-wall stability limit (3).
*Supported by US DOE Contract DE-SC0018623.
(1) A. Piccione, et al., accepted by Nuclear Fusion (2020)
(2) J.W. Berkery, et al., Physics of Plasmas 24 (2017) 056103
(3) J.W. Berkery, et al., Physics of Plasmas 17 (2010) 082504
| Affiliation | Columbia University |
|---|---|
| Country or International Organization | United States |
