Speaker
Description
This paper first studies the coupling effects between the impurities and the background plasma under BOUT++ framework by extending the six-field two-fluid MHD model 1. The extended model is applied to study the effect of pedestal Li impurity on ELMs during real-time Li powder injection. The extended BOUT++ MHD model is first validated by the good agreement between analytical results and numerical ones over a linear model. The obtained results can help deepen understanding the physical mechanism of ELM suppression resulting from impurity. The validated extended MHD model is then being applied to simulate the ELM evolution in its nonlinear phase.
During the operation in the current tokamak devices, some amount of various types of impurities inevitably penetrates the separatrix and enters the core plasma region, then changes the background plasma, and subsequently affects the MHD instabilities. Therefore, it is necessary and important to understand the physical mechanism behind by constructing reliable models and developing corresponding numerical codes. To couple the effect of impurity equilibrium on the background plasma into the BOUT++ MHD model, we redefine the vorticity by introducing the contribution of impurity to the vertical component of ion velocity and modify the gyro-viscous term by integrating the impurity contribution into the vorticity equation. Using this extended model, we take only diamagnetic drift into account for deriving analytical dispersion relation of strong peeling-ballooning case, and take into account the contributions of diamagnetic drift, resistivity, gyro-viscosity, and the effect of cross term for numerical simulation.
Based on the obtained dispersion relation, we can know that the increment in the plasma mass density due to the Li ions present in the pedestal region not only leads to a stabilizing effect on the ideal peeling-ballooning mode, but also weakens the ion diamagnetic stabilization, an indirectly destabilizing effect on the instability. These two opposite effects compete with each other, as shown in Fig. 1: when the diamagnetic frequency is close to the ideal instability growth rate, the weakening effect of impurity on the ion diamagnetic stabilization becomes dominant; when the diamagnetic frequency is much less than the ideal instability growth rate, the stabilizing effect of impurity on the ideal peeling-ballooning mode is dominant. After further considering the reducing temperature due to the existence of pedestal impurity, the background temperature drops. This cooling effect helps stabilize the peeling-ballooning mode more effectively through reducing the diamagnetic frequency and the ideal instability growth rate by a same percentage.
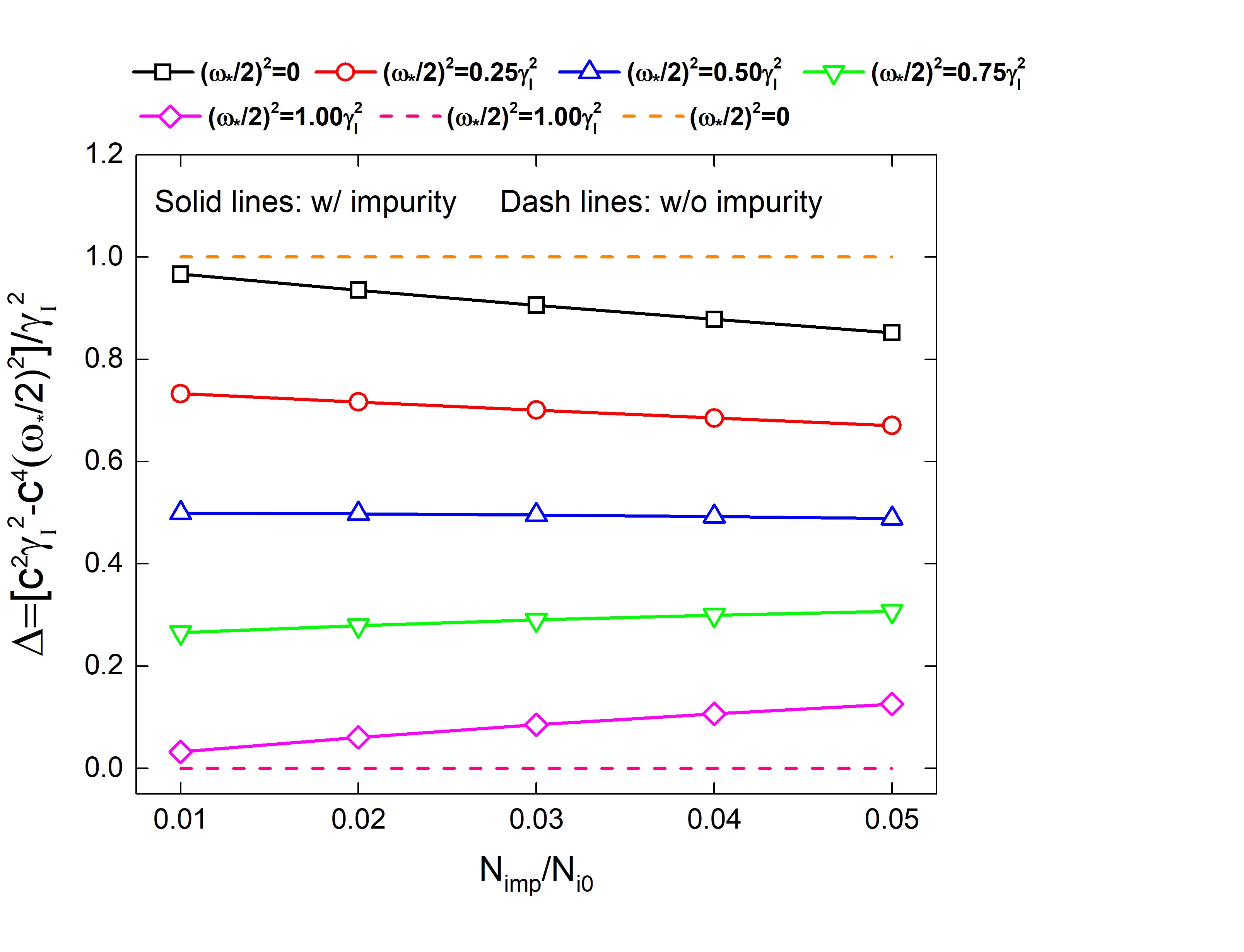
To understand how the impurity affects the growth rate of individual mode, we present the corresponding numerical results in Figs. 2 and 3. As can be seen, the simulation results have a good agreement with the analytical results, which validates the reliability of this extended MHD model. Note that, in the case of strong peeling-ballooning mode, the effect of resistivity is negligibly small. Based on this finding, we further consider the effect of gyro-viscosity and the cross term in the vorticity definition, respectively, and carry out simulations. The result shows that the pedestal Li ions have a negligible effect on strong peeling-ballooning mode through the additional gyro-viscos term and cross term of impurity in the evolved vorticity equation.
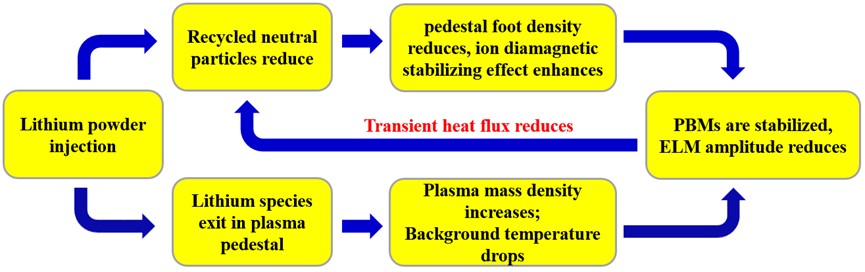
Based on the extended model and the aforementioned findings, we further advance understanding the physical mechanism for ELM suppression by impurities, which originates from the ELM suppression mechanism proposed in 2 for assessing the Li wall conditioning effects on ELMs. The mechanism is shown schematically in Fig. 4. With the Li conditioned wall, some amount of Li species inevitably come into the scrape-off-layer region and some of them finally enters the plasma pedestal. These pedestal Li ions then stabilize peeling-ballooning mode to some degree, as the ion diamagnetic stabilizing effect is not strong enough to stabilize the ideal peeling-ballooning mode completely. In addition, the recycling neutral particles reduces from the PFCs with Li conditioning wall, leading to the decrease in the density at the pedestal base and consequently, the enhancement in the ion diamagnetic stabilizing effect, which can further stabilize peeling-ballooning mode 2. It is found that either the pedestal Li ions or the reduced edge recycling, or the combination of them reduces the ELMs amplitude. In addition, as the ELMs amplitude goes down, the transient heat flux subsequently reduces,The reduction of transient heat flux leads to the decrement of the neutral recycling at the wall and target plates. Thus, a positive feedback loop takes place, and maintains until the density at the pedestal base approaches the threshold value for stabilizing peeling-ballooning mode completely 2.
The remaining work of this paper is to carry out the nonlinear simulation of strong peeling ballooning mode case. This work is on the way now and the new results will be reported on the coming conference.
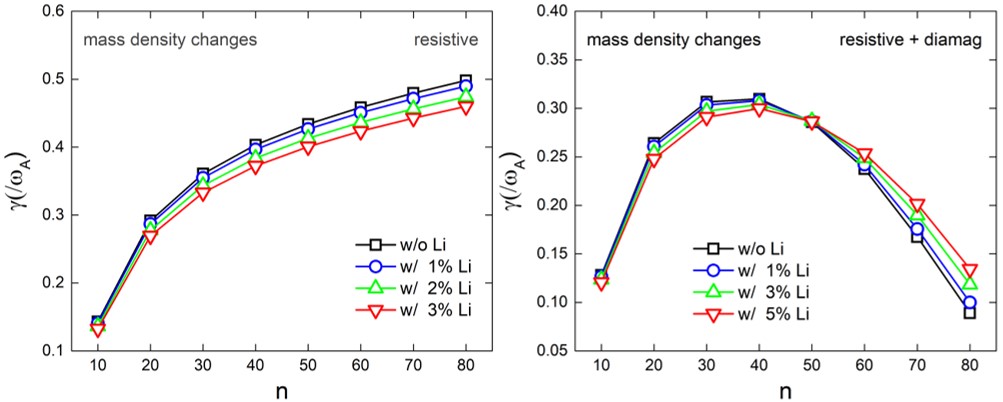
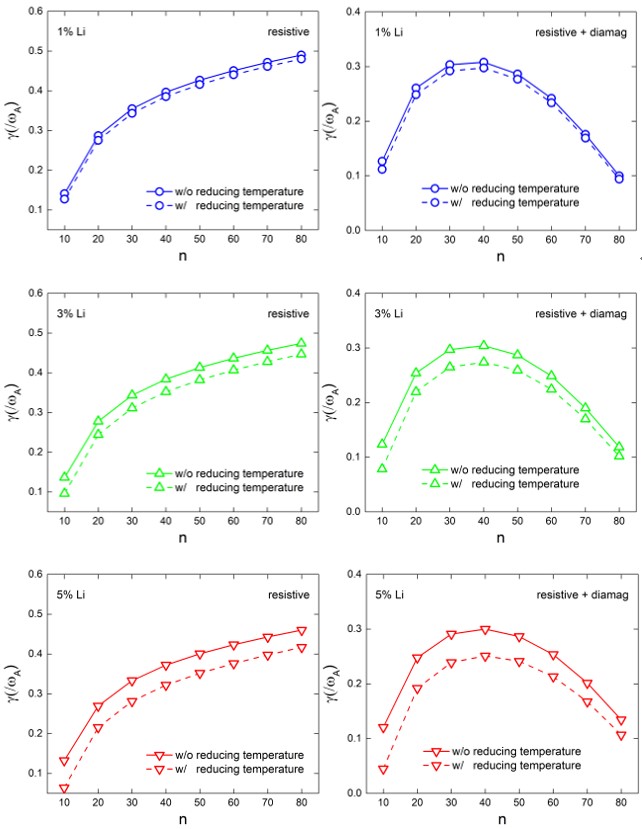
Reference:
1 T. Y. Xia, et al, “Six-field two-fluid simulations of peeling–ballooning modes using BOUT++”, Nucl. Fusion 53 (2013) 073009
2 Y. Ye, et al, “Experimental study on low recycling no-ELM high confinement mode in EAST”, Nucl. Fusion 59 (2019) 086044.
| Affiliation | Key Laboratory of Materials Modification by Laser, Ion, and Electron Beams (Ministry of Education), Dalian University of Technology, Dalian 116024, China |
|---|---|
| Country or International Organization | China |
