Speaker
Description
As a promising strategy, quiescent H-mode (QH-mode) offers tokamak plasma scenarios without edge localized modes (ELMs) but with constant plasma density and radiated power. This type of ELM-free H-mode regime is often achieved at relatively low plasma density in experiments, and is found to be accompanied by the presence of edge harmonic oscillations (EHOs), which are believed to provide necessary transport to eliminate ELMs by the plasma self-regularization dynamics. The saturated kink-peeling mode has been suggested as a possible candidate for EHO. According to this scenario, an edge localized kink-peeling instability, with the dominant toroidal mode number typically below 3 ($n\leq3$), is non-linearly saturated by the plasma flow, thus leading to EHO.
In this work, we perform a systematic numerical investigation of various physical effects on the kink-peeling instabilities in a DIII-D QH-mode plasma from discharge 157102, utilizing the MARS-F/K/Q suite of code $[1][2][3]$. These include the wall eddy current effect, the influence of the plasma resistivity on the mode stability, the kinetic effects associated with thermal particle drift motions, the effect of plasma pedestal toroidal flow and flow shear, and finally the dynamics of self-consistent interaction between the plasma flow and the kink-peeling mode. Quantitative comparison has also been made between modeling and experimental data.

With the Spitzer model assumed in this study, we find that the computed $n=1$ and $n=2$ kink-peeling growth rate is well approximated by an analytic scaling of $S^{-1/3}$, similar to that for the edge localized infernal mode $[4]$.
With all the drift kinetic physics included in this study, namely (i) the precessional drift resonance of trapped ions and electrons ($\alpha_D$), (ii) the bounce resonance of trapped ions ($\alpha_B$), and (iii) the transit resonance of circulating ions ($\alpha_C$), MARS-K modeling finds destabilizing effect on the low-n kink-peeling mode (Fig.1(a)). Kinetic effects also modify the mode eigenfunction, by reducing the core mode components (Fig.1(c)) and by shifting the peak location of the perturbation near the plasma edge (Fig.1(d)).
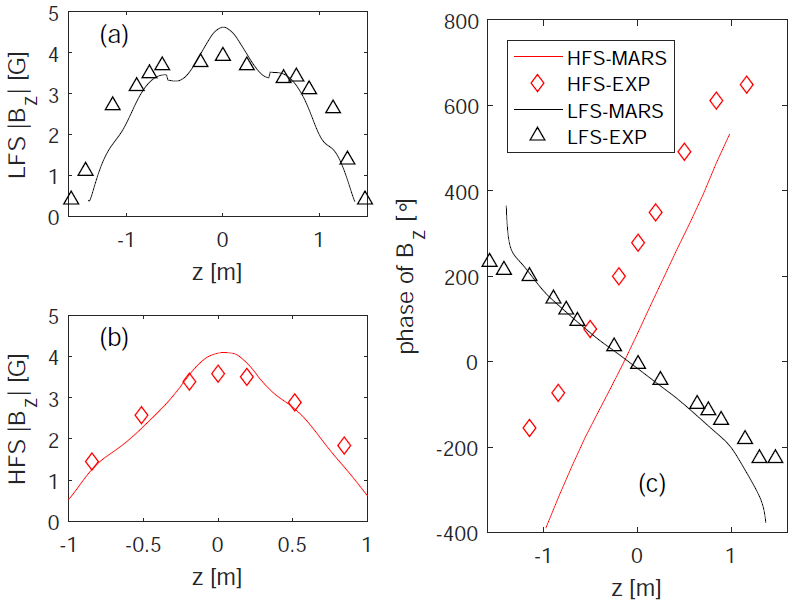
The computed mode eigen-structures are also compared with experimental measurements. Figure 2 shows the amplitude and toroidal phase of the n=1 magnetic fluctuations associated with poloidal magnetic sensors from both low and high field sides of the torus. The modeled results agree reasonably well experiments, except for a slight systematic phase shift for the high field side magnetic signal.
The MARS-Q initial value quasi-linear simulations reveal that several plasma parameters sensitively affect the non-linear interaction between the plasma flow and the kink-peeling instability. These include the momentum diffusion coefficient $\chi_M$ as well as the amplitude $A_0$ of the initial perturbation. One example is shown in Fig.3, where we fix $\chi_M$=1m$^2$/s and vary $A_0$ $[5]$. The time traces of the perturbed $m/n=6/1$ radial field component, at the $q=6$ rational surface, show that different initial perturbation amplitudes result in similar level of the saturated mode amplitude (Fig.3(a)). The simulated saturation time scale, however, is different (Fig.3(a-b)). The time behavior of the flow damping near the plasma edge (at the q=6 surface as shown in Fig.3 (b)) shows a similar pattern independent of the saturation time scale (Fig.3 (b)). The edge flow always decreases to a minimal value of about -10 krad/s, before recovering to about 0 krad/s level.
Significant change of the plasma edge rotation profile (and rotation shear) occurs during the saturation of the kink-peeling mode, as shown by Fig.3(c) where $A_0=5\times10^{-8}$ is assumed. Further comparison of the time traces of the net torque amplitude (Fig.3(d)) shows that the dominant contribution to the flow variation comes from the net Reynolds stress torque and resonant electromagnetic ($j\times b$) torque.

Reference
$[1]$ Y. Q. Liu, et al, Phys. Plasmas 7, 3681 (2000).
$[2]$ Y. Q. Liu, et al, Phys. Plasmas 15, 112503 (2008).
$[3]$ Y. Q. Liu, et al, Phys. Plasmas 20, 042503 (2013).
$[4]$ G. Q. Dong, et al, Phys. Plasmas 24, 112510 (2017).
$[5]$ G. Q. Dong, et al, Nucl. Fusion 59, 066011 (2019).
| Affiliation | Southwestern Institute of Physics |
|---|---|
| Country or International Organization | China |
