Speaker
Description
After the IAEA-FEC 2016 presentation (1) showing that the midplane-mapped heat-load width $\lambda_q^{XGC}$ predicted by the XGC1 edge-gyrokinetic-code (2) for the full-current ITER is $\stackrel{>}{\sim}6\times$ wider than the experimental-data based formula $\lambda_q^{Eich}$ (PRL 2011) while the same code reproduces $\lambda_q^{XGC}\simeq\lambda_q^{Eich}$ for the present experiments, a major effort has been devoted to resolving this puzzle: Several new and higher-resolution extreme-scale predictive simulations and indepth physics studies have recently been performed. A machine learning program is then used to discover hidden kinetic parameters and produce a new predictive formula encompassing the Eich formula, the full-current ITER result and other anomalous XGC prediction results. It is found that the hidden parameters are associated with the low neoclassical $E\times B$ flow in the 15MA ITER edge (3,1) and the arousal of the trapped electron mode (TEM) turbulence across the magnetic separatrix.
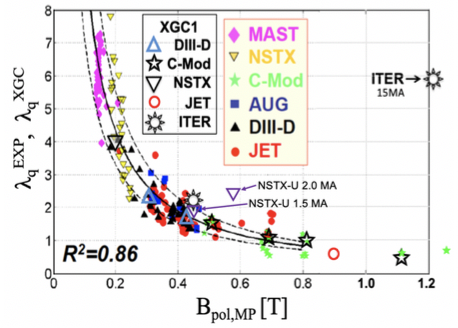
For a full-current ITER H-mode operation at $I_p=15$MA with $q_{95}=3$, we have $\lambda_q^{Eich}(=0.63B_{pol,MP}^{-1.19}) \stackrel{<}{\sim}1mm,$ where $B_{pol,MP}$ is the poloidal magnetic field at outboard midplane separatrix. At this range of $\lambda_q$, which is about a factor of 5 narrower than the design value, the divertor operation must be at least in semi-detached conditions where the plasma pedestal density can easily reach the Greenwald density limit and the disruption-free operation becomes difficult.
However, it is questionable if such a simple extrapolation from the present experimental data is valid since the 15MA ITER edge may obey fundamentally different physics, especially when the eddy shearing effect on the microturbulence by neoclassical ExB flow is expected to be much weaker due to negligible ion banana width compared to plasma size (3,1). As can be seen from Fig. 1, all $\lambda_q^{XGC}$ predictions on three US tokamaks (NSTX, DIII-D and C-Mod) agree with the Eich formula ($\lambda_q^{Eich}$, solid line) within experimental error bar (dashed lines). However, when the same code is applied to the 15MA ITER edge plasma, the XGC-predicted $\lambda_q^{XGC}$ was $\stackrel{>}{\sim} 6\lambda_q^{Eich}$. This anomalous result has been left as an unsolved puzzle since IAEA-FEC-2016 that required a major undertaking including new extreme-scale simulations and in-depth physics studies.
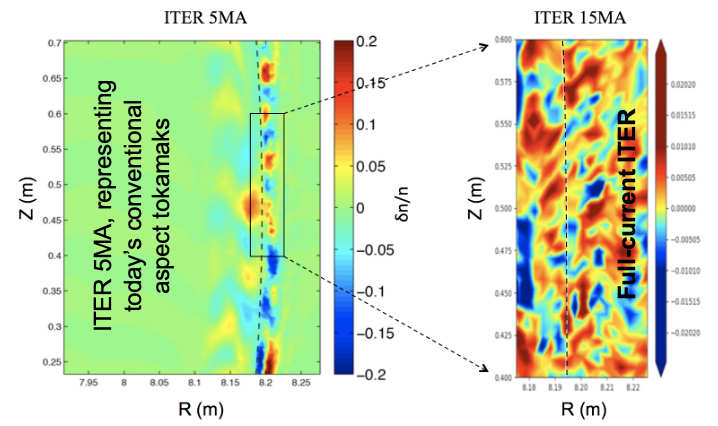
Several critical and higher resolution XGC1 simulations have recently been performed, which include the first H-mode scenario plasma in ITER with $I_p=5$MA. This plasma has $B_{pol,MP}=0.43T$ that is similar to a high field DIII-D plasma ($\ast$ mark in Fig.1), while the plasma size is the same as for 15MA ITER. We find $\lambda_q^{XGC}\simeq 2.2mm$, similar to $\lambda_q^{Eich}=1.7 mm$. This result denies the conjecture from some physicists that the pure size effect could be responsible for the large $\lambda_q^{XGC}$ in 15MA ITER. Comparison of the turbulence pattern between the 5MA and 15MA ITER cases reveals an interesting physics difference: In the 5MA case, turbulence patterns across separatrix are isolated and “blobby,” as in all the present tokamaks that obey the Eich scaling, while the patterns become a radially connected “streamer” type in the 15MA case (Fig.2).
In a JET 4.5MA plasma that is the closest experimental plasma to the 15MA ITER in the sense of both size (half the linear size of ITER) and the poloidal magnetic field $B_{pol,MP}$ (= 0.89T, compared to 1.21T), XGC1 finds $\lambda_q^{XGC}=0.64mm$, which is again within the experimental error bar from $\lambda_q({Eich}=0.72mm$ (see Fig.1). Also, the turbulence across the separatrix remaines blobby. The compact tokamak NSTX-U is under construction to raise the plasma current to 2MA, in which the edge electrons become weakly collisional. In this plasma, XGC1 finds that $\lambda_q^{XGC}\sim 2\lambda_q^{Eich}$ (Fig.1) with the edge turbulence becoming streamer type. However, in a 1.5MA NSTX-U model plasma, XGC finds $\lambda_q^{XGC}\sim \lambda_q^{Eich}$ (Fig.1). One noticeable difference in the dimensionless parameter of 1.5MA plasma from 2MA is that the plasma is collisional at separatrix. These NSTX-U results add to the puzzle that needs to be resolved together with the full-current ITER case.
More influentially to this study, experiments at C-Mod raised $B_{pol,MP}$ values near and somewhat above the 15MA ITER value (4), and found that $\lambda_q$ still follows $\lambda_q^{Eich}$ (see two example experimental results in green stars in Fig.1). We have simulated one of theses high current discharges that has a similar $B_{\rm pol,MP}$ value (1.11T) to that of ITER (1.21T). We find $\lambda_q^{Eich}=0.4mm$ that is even somewhat smaller than $\lambda_q^{Eich}= 0.56mm$. As a result, the XGC1’s solution becomes double valued around the full-current ITER $B_{\rm pol,MP}$ if $B_{\rm pol,MP}$ is used as the sole parameter, and suggests hidden parameters that were missing in the regression study by Eich et al.
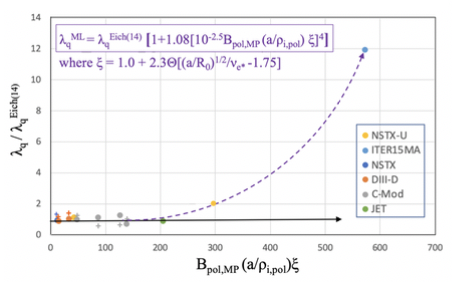
In an effort to find the hidden parameters and a scaling formula that will resolve the double-valuedness and encompass all the predictive simulation results including the 15MA ITER, the 2MA NSTX-U, the $\lambda_q^{Eich}$ formula, and the experimentally measured $\lambda_q^{Exp}$ values corresponding to the simulation points, we utilized the AI-based modeling engine Eureqa (5). Eureqa works by creating random equations from the input data through a technique called “evolutionary search” and suggest equations that fit the data with various accuracy.
Among many Eureqa-produced formulas, the simplest and physically meaningful formula is identified as
$\lambda_q^{ML}=0.63B_{pol,MP}^{-1.19} [1.0 + 1.08\times 10^{-10} (B_{pol,MP}\; a/\rho_{i,pol} \xi)^4]\;\;\; (A)$
with RMS error 0.19, where $\xi=1.0+\alpha \; \Theta [(a/R)^{1/2}/\nu_{e*}- \beta]$ with $\alpha=2.3, 1.7<\beta<1.9$, and $\Theta$ the heavyside step function. In this formula, there is a long distance between the C-Mod and the 15MA ITER $\lambda_q$ points, well-resolving the double-valuedness (Fig.3). A more definitive $\beta$ number or a smooth function for $\Theta$ could not be determined due the limited number of the off-$\lambda_q^{Eich}$ points. The form of the function $\xi$, a highly simplified criterion for collisionless TEM instability, has been manually instructed from the XGC observation that whenenver we have an enhanced $\lambda_q^{XGC}$, the edge turbulence across sepatrix becomes streamer-type TEM turbulences (Fig.2). Convincing XGC1 evidences for the TEM turbulence, instead of blobs, across separatrix in 15MA ITER plasma exist: For example, 1) a linear analysis without $E\times B$ shearing shows unstable TEMs just inside the separatrix, 2) a cross-correlation study of XGC1 data finds a distinctive non-adiabatic electron behavior, and 3) an unsupervised machine learning study shows a high-degree of correlation beteween trapped electrons and turbulence. The formula (A) is physically meaningful because the parameter $B_{pol,MP}\; a/\rho_{i,pol}$ is related to the ion banana width and the neoclassical $E\times B$ shearing rate ($\propto \rho_{i,pol}/a$). Both of them have sensitive influence on the turbulence structure. Also the electron collision frequency in all the existing tokamak edge plasmas that obey the $\lambda_q^{Eich}$ is not low enough to provoke the collisionless TEM turbulence.
More number of predictive simulations (including the on-going study for 12.5MA ITER, to be presented at IAEA-FEC2020) and possible experimental data in the gap region could improve the accuracy of Eq.(A) (especially, of $\beta$ and $\Theta$). A future improved formula is, however, not expected to be much different from Eq. (A), which describes all the $\lambda_q^{XGC}$ results obtained so far, encompassing the full-current ITER, and is consistent with the kinetic physics discoveries and understandings.
This study is mostly funded by US DOE, with computing resources provided by OLCF.
(1) Chang C.S., Ku S., Loarte A. et al., Nucl. Fusion 57, 116023 (2017)
(2) Ku S., Chang C.S. et al., Phys. Plasmas 25, 056107 (2018)
(3) D.R. Hatch, M. Kotschenreuther, Nucl. Fusion 57, 036020 (2017)
(4) Brunner D., LaBombard B. et al., Nucl. Fusion 58, 094002 (2018)
(5) Product of Nutonian, now acquired by DataRobot.
| Affiliation | Princeton Plasma Physics Laboratory |
|---|---|
| Country or International Organization | United States |
