Speaker
Description
In this paper, we present the recent experimental results of cross phase influence on turbulent momentum and particle transport in the edge of HL-2A tokamak. The mathematical expressions for cross phases are derived in Fourier domain. The fluctuations and turbulent flux are measured by Langmuir probes. For Reynolds stress, prominent phase scattering in the strong shear layer is found, which indicates a phase slipping state as predicted by theory. With ECRH, the cross power is more concentrated in the high $ \gamma cos(\varphi) $, which shows an agreement with the dynamics of spectral symmetry breaking in the development of poloidal torque. For particle flux, phase scattering increases with RMP, which could be induced by field line stochastisation due to magnetic flutter. Comparative statistical study shows that, fluctuations in particle flux exhibit a big deviation from Gaussian distribution, while fluctuations in Reynolds stress don’t. This suggests that edge transport models based on quasi-linear theory need to be reconsidered. This may be related to L-H transition physics. The cross phase dynamics may be also relevant to I-mode, which shows L-mode like density profiles, but H-mode like temperature profiles, with phase slipping in heat flux but locked in particle flux.
High confinement regimes are expected to be the operation scenarios of future fusion reactors such as ITER. A fundamental feature of these regimes in magnetic confinement devices is the formation of transport barriers, and the dramatically decreased turbulence transport. The primary physics involved in transport reduction is the effect of $ E\times B $ velocity shear owing to a decrease in the intensity of fluctuations, as well as the change in the cross phase between them $ {^1} $. The transient increase in $ E\times B $ sheared flows plays an important role in the L-H transition. The turbulent flux of momentum—Reynolds stress—is a mechanism thought to be responsible for the generation of sheared flow driven by turbulence $ {^2} $. Reynolds stress and fluxes are sensitive to cross phase. However, usual quasilinear theory does not treat phase as dynamic. Study of cross phase influence on turbulent transport and the interaction between sheared flow and cross phase, is significant for understanding the high confinement regimes.
Ensemble-averaged Reynolds stress or particle flux is written as the product of fluctuation intensities and a cross phase factor: $ 〈 \tilde{v} _r \tilde{v }_\theta 〉=\sigma_{ \tilde{v }_r }\cdot \sigma_{ \tilde{v} _\theta}\cdot X_{RS} $, $ 〈 \tilde{n} \tilde{v}_r 〉=\sigma _{\tilde{n}} \cdot \sigma_{ \tilde{v }_r} \cdot X_{PF} $. By using Fourier transform, the mathematical expressions for $ X_{RS} $ and $ X_{PF} $ are derived:
$ X_{RS}=\frac{\sum_\omega P_{ \tilde{v }_r \tilde{v }_r}(\omega)^{1/2} P_{ \tilde{v }_\theta \tilde{v }_\theta}(\omega)^{1/2} \gamma_{ \tilde{v }_r \tilde{v }_\theta} (\omega)\ cos\varphi_{ \tilde{v }_r \tilde{v }_\theta}(\omega)}{(\sum_\omega P_{ \tilde{v }_r \tilde{v }_r}(\omega))^{1/2}\ (\sum_\omega P_{ \tilde{v }_\theta \tilde{v }_\theta}(\omega))^{1/2}}, $ (1)
$ X_{PF}=\frac{\sum_\omega P_{ \tilde{n } \tilde{n } } (\omega)^{1/2} P_{ \tilde{v }_r \tilde{v }_r}(\omega)^{1/2} \gamma_{ \tilde{n } \tilde{v }_r}(\omega)\ cos\varphi_{ \tilde{n } \tilde{v }_r} (\omega)}{(\sum_\omega P_{ \tilde{n } \tilde{n }}(\omega) )^{1/2}\ (\sum_\omega P_{ \tilde{v }_r \tilde{v }_r} (\omega) )^{1/2}}. $ (2)
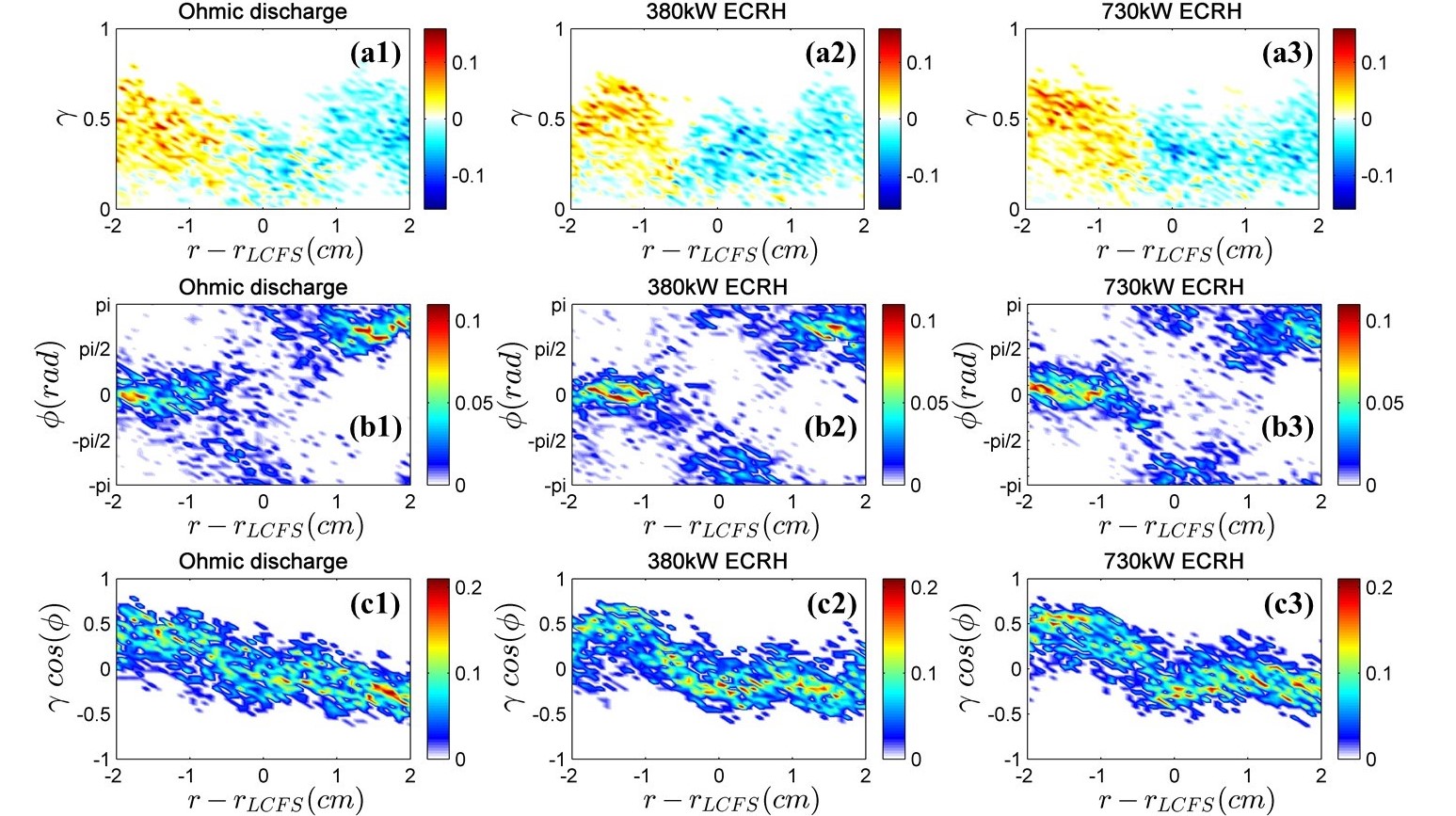
Figure 1 shows the cross phase evolution of Reynold stress in Ohmic and ECRH heated L-mode discharges. Figure 1(a1-a3) show the normalized cross power profile between $ \tilde{v }_r $ and $ \tilde{v }_\theta $, and its distribution on coherence $ \gamma $. $ \gamma $ drops in the strong shear layer near [-1,1] cm. This shows the turbulence decorrelation by the sheared flow. Figure 1(b1-b3) show the normalized cross power distribution on cross phase angle $ \varphi $. The phase scattering in the strong shear layer is larger than other regions. The phase angle tends to distribute in [-$ \pi $/2,$ \pi $/2] at [-2,-1] cm, and [$ \pi $/2,$ \pi $] at [1,2] cm. This is consistent with a novel theory, which indicates two different states of the cross phase: slipping in strong shear regimes and locked in weak shear regimes $ {^3} $. Figure 1(c1-c3) show the cross power distribution on X factor $ \gamma cos(\varphi) $. X factor changes from negative to positive from SOL to edge. With ECRH, the cross power is more concentrated in the high X factor region. This exhibits good agreement with the dynamics of spectral symmetry breaking in the development of poloidal torque $ {^4} $.
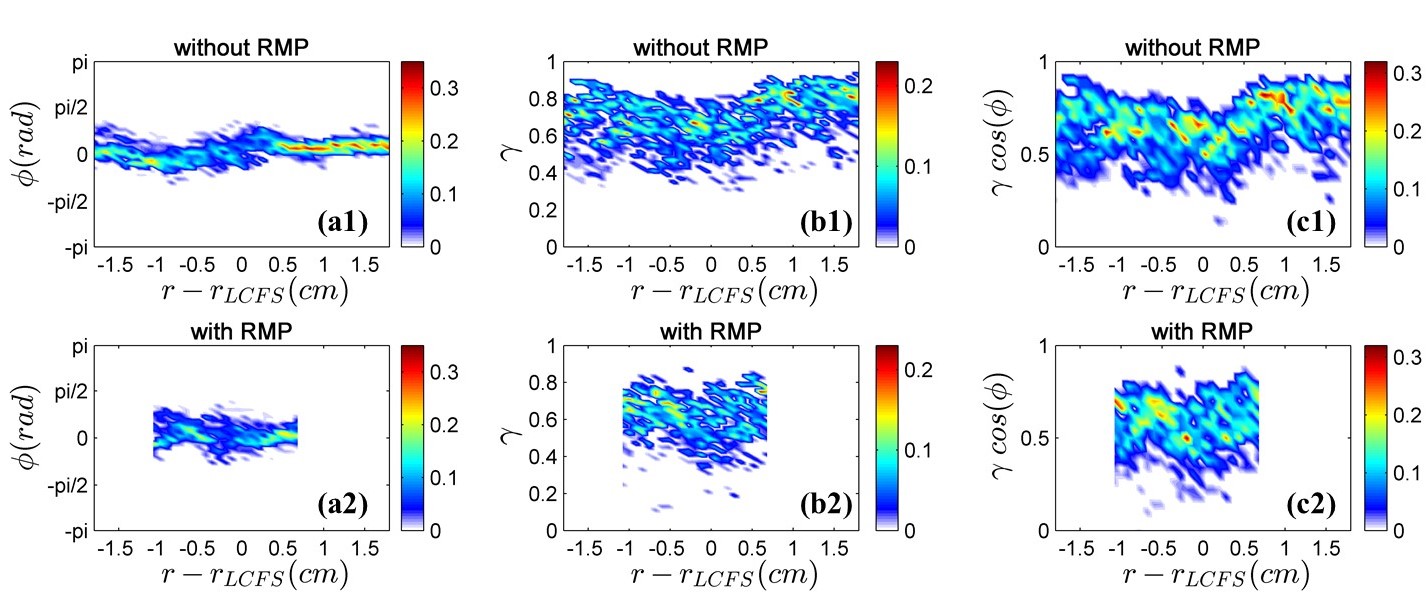
Figure 2 shows the cross phase evolution of particle flux in Ohmic discharges with and without RMP. Figure 2(a1) shows that the cross power is more concentrated in the positive $ \varphi $~0.2 at [0.5,1.5] cm, and concentrated in the negative $ \varphi $~-0.2 at [-1.5,-0.5] cm. The phase scattering in the strong shear layer near [-0.5,0.5] cm is larger than other regions. Figure 2(a2) and (b2) show that , with RMP, the phase scattering increases and the cross power is more concentrated in the higher coherence. This could be induced by field line stochastisation due to magnetic flutter.
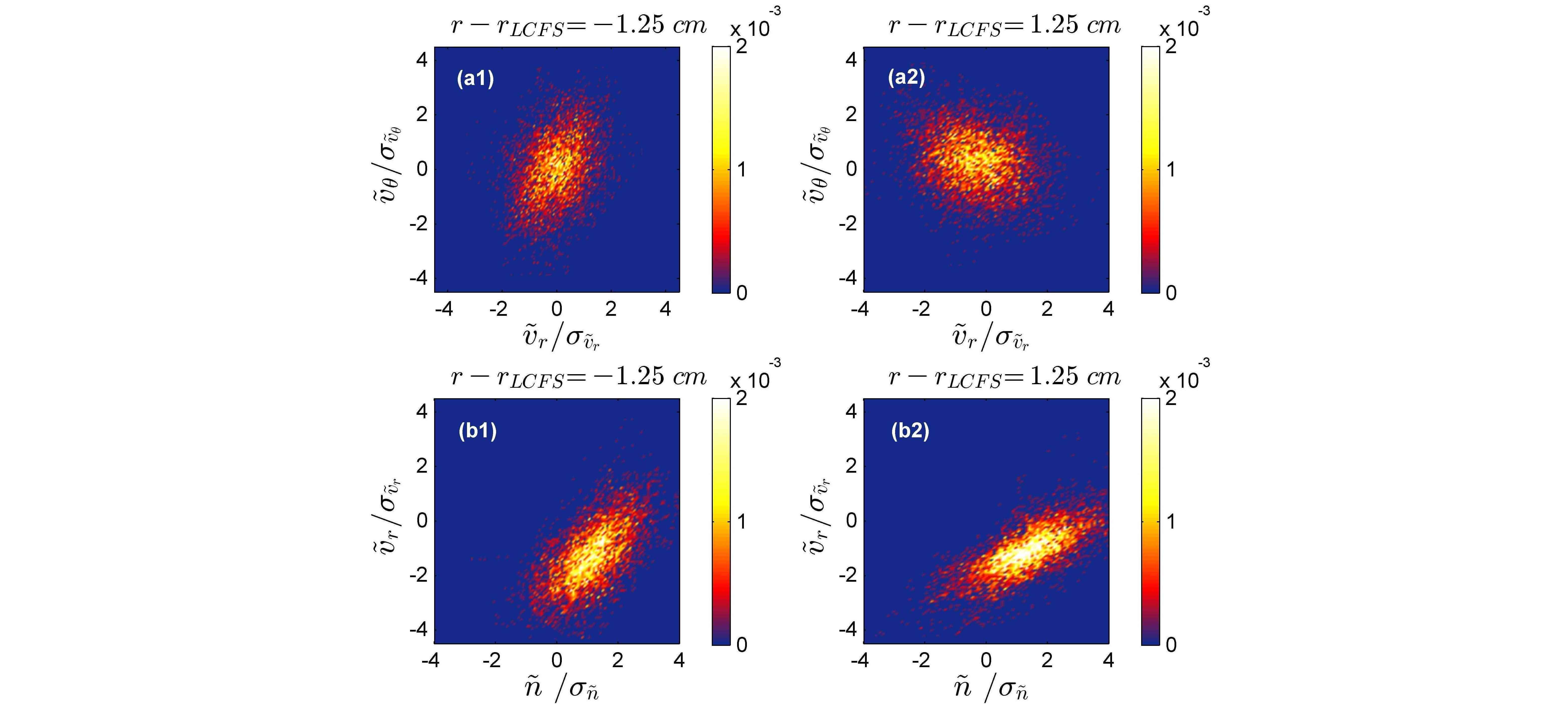
Figure 3 shows the joint PDF of $ \tilde{v }_r $-$ \tilde{v }_\theta $ and $ \tilde{n } $-$ \tilde{v }_r $ at ±1.25cm in Ohmic discharges. Unlike the joint PDF of $ \tilde{v }_r $ and $ \tilde{v }_\theta $, the center of $ \tilde{n} $-$ \tilde{v }_r $ PDF shows a large deviation from (0,0) point. This indicates the distributions of fluctuations have a big deviation from Gaussian whose skewness should be 0. Particle flux is necessarily nonlinear in $ \nabla n $, leading to an asymmetric PDF tail due to intermittent transport events. In contrast, the Reynolds stress is secondary to the particle flux. It has weaker $ \nabla n $ dependence, and so is closer to Gaussian. More statistical studies (skewness, kurtosis, Hurst parameter) of cross phase are planned for future work.
References
1 Boedo, J.A., et al., Physical Review Letters, 2000. 84(12): p. 2630-2633.
2 Diamond, P.H. and Y.B. Kim, Physics of Fluids B, 1991. 3(7): p. 1626-1633.
3 Guo, Z.B. and P.H. Diamond, Physical Review Letters, 2015. 114(14): p. 145002.
4 Long, T., et al., Nuclear Fusion, 2019. 59(10): p. 106010.
| Affiliation | Southwestern Institute of Physics |
|---|---|
| Country or International Organization | China |
