Speaker
Description
In tokamak discharges there are often saturated Alfven modes (1). They are destabilized by gradients of the high energy particle population, so are to be expected in discharges with a significant alpha particle population, such as expected in ITER (2) or any fusion device. These modes may produce only a small local flattening of the particle distribution, or if the number and amplitude be large enough, cause particle loss when the resonances associated with the modes overlap sufficiently to cause chaotic pathways for redistribution (3).
There are two types of events in which the \alfven modes have rapid significant effect on the high energy particle distribution, chirping modes and avalanches. A chirp is a complex frequency modulation of a single mode, causing also local particle distribution modification (4,5). An avalanche is a combination of a few modes to produce a large scale cascade of particles, leading to particle loss and even to discharge termination (6). These phenomena have been simulated using the guiding center code ORBIT (7) using a $\delta f$ formalism (8,9,10), which is able of capturing details of large phase-space structures. While not able to follow the large scale modification of the particle distribution or nonlinear mode coupling dynamics involved in the final stages of these events, this formalism is adequate to investigate the conditions for the onset of these phenomena and the initial behavior, and hence provide information as to how they can be avoided. Simulations of an NSTX (11) chirp and an avalanche are shown in Figs. 1 and 2.
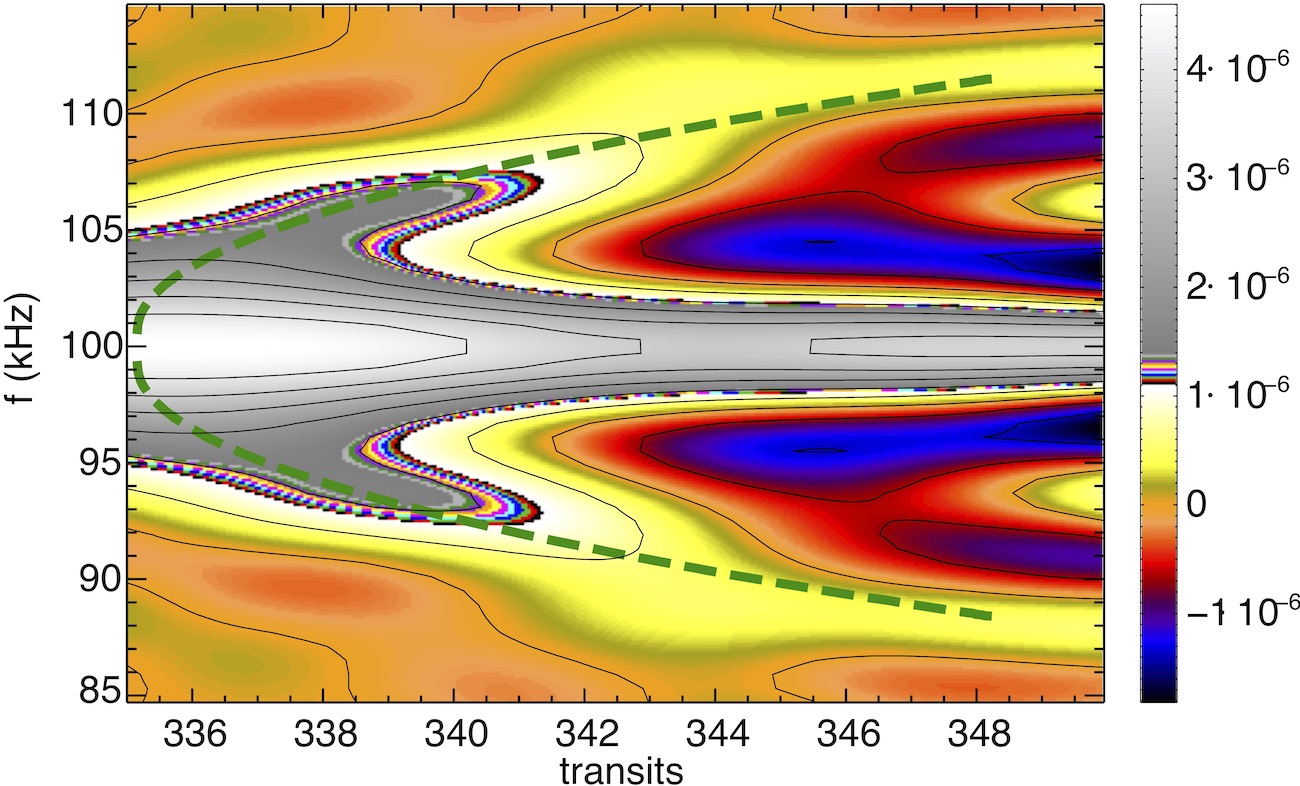
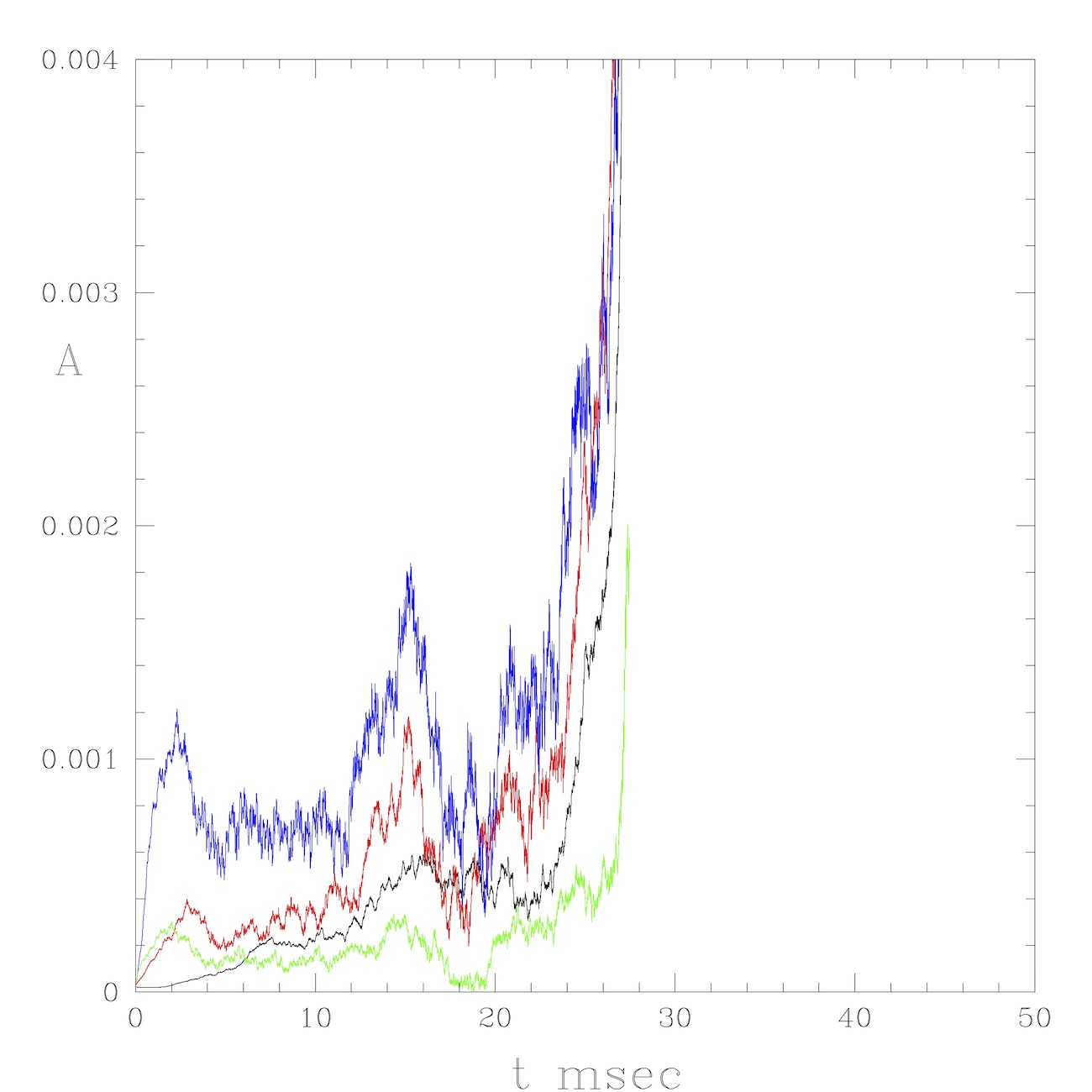
An energetic particle driven \alfven mode has energy transferred from the particle distribution to the mode through distribution flattening within a resonance, producing the linear growth rate $\gamma_L$, accomplished by the fine scale phase mixing in the resonance. Once the distribution has been flattened, without collisional replenishment of the density gradient, mode drive ceases. In addition, a mode can be strongly damped due to the continuum, trapped particle effects, Landau damping and radiation, with total damping $\gamma_d$. We find that chirping occurs when a mode experiences small collisions and strong damping, such as could be due to a small equilibrium change causing contact with the continuum. A chirp of an Alfven mode involves complex particle organization so as to extract energy from the particle density gradients at the edge of the resonance island, producing a particle clump and a hole and frequency sidebands departing from the original mode frequency.
Avalanches depend on the overlap of resonances located so as to provide a path for large scale particle redistribution. Thus the possibility of avalanche depends on the nature and magnitude of the resonances associated with the modes. If this path extends to the plasma edge, particle loss can occur. During a discharge, the drive of the modes can be increasing due to changes in the high energy particle distribution. In addition, we find that the size of the resonances increases with decreasing Alfven mode frequency, inversely proportional to the square root of the plasma density. Thus the increase in plasma density and the increase in high energy particle density can both contribute to the onset of an avalanche. We show that the location and nature of the existing resonances can be determined using the equilibrium and particle distribution data, and hence the possibility of avalanche and possible means of avoidance, without extensive numerical simulation.
Acknowledgement: This work was supported by the US Department
of Energy (DOE) under contract DE-AC02-09CH11466.
References:
(1) C. Cheng, L. Chen, and M. Chance, Annals of Physics 161, 21 (1985).
(2) The iter project, http://www.cad.cea.fr/gb/activites/fusion/ITER.php.
(3) C.S.Collins,W.W.Heidbrink,andetal(DIII-Dteam),Phys. Rev. Lett. 116, 095001 (2016).
(4) E. Fredrickson, R. Bell, D. Darrow, and et al, Phys. of Plasmas 13, p056109 (2006).
(5) W. W. Heidbrink, Plasma Phys. Control. Fusion 37, 937 (1995).
(6) E. Fredrickson, N. Crocker, D. Darrow, and et al, Nuclear Fusion 53, 013006 (2013).
(7) R. B. White and M. S. Chance, Phys. Fluids 27, 2455 (1984).
(8) R. B. White, The Theory of Toroidally Confined Plasmas (Imperial College Press, 2014).
(9) R. B. White, V. N. Duarte, N. N. Gorelenkov, and et al, Phys. of Plasmas 26, 092103 (2019).
(10) R. B. White, V. N. Duarte, N. N. Gorelenkov, and et al., Phys. of Plasmas x, x (2020).
(11) S. M. Kaye, M. Bell, R. Bell, S. Bernabei, J. Bialek, and et al, Nucl. Fusion 45, S168 (2005).
(12) H. L. Berk, B. N. Breizman, and V. Petviashvili, Phys Lett A 6, 3102 (1999).
| Affiliation | Princeton Plasma Physics Laboratory |
|---|---|
| Country or International Organization | United States |
