Speaker
Description
Introduction
A powerful method for diagnosing runaway electrons in tokamak experiments is to measure the synchrotron radiation that the relativistic electrons emit. The radiation intensity depends on the electron energy, pitch angle as well as the background magnetic field, and using a spatially resolved diagnostic, such as a camera, allows the spatial distribution of electrons to be studied. Synchrotron radiation is therefore sensitive to the details of certain parts of the electron distribution function, making it ideal for validating kinetic models for runaway electrons. The detailed predictions obtained from kinetic runaway models can otherwise be difficult to test experimentally, as one must then usually rely on signals which are averages of the full distribution function.
Principles
Synchrotron radiation is the ultra-relativistic extension of cyclotron radiation, and is as such emitted almost exactly along the particle velocity vector due to relativistic beaming effects. This means that while usual cyclotron radiation would give rise to a familiar torus of radiation on a camera image, a camera observing synchrotron radiation would only see one or a few distinct ``patches'' of radiation from one side of the torus, corresponding to the locations in the device where the electrons' velocity vectors are pointing at the synchrotron camera. This complicated dependence of the synchrotron patches on the background magnetic field means that a simulation tool taking the magnetic field geometry into account must be used, and for this reason we have developed the synthetic synchrotron diagnostic SOFT [1]. With SOFT, it is possible to simulate all types of synchrotron diagnostics used in present-day experiments, including visible- and IR cameras [2], spectrometers [3] and MSE polarimeters [4].
Dominant particles
Generally, electrons with larger pitch angles and higher energies emit more synchrotron radiation. Conversely, most runaway electrons tend to have very small pitch angles, and if the population has been sufficiently multiplied through large-angle collisions, the number of particles with energy $\gamma$ decreases exponentially with $\gamma$. As a result, only a small subset of the runaway electron population contributes significantly to any synchrotron radiation measurement, corresponding to the particles that dominate emission of synchrotron radiation. This small region in momentum space is therefore the only region which we can hope to explore in true detail, although with the help of state-of-the-art runaway models, this is often sufficient to gain some understanding for the kinetic processes affecting the majority of electrons in the population.
A synchrotron image or spectrum usually shows clear similarities to the image or spectrum that would result if all electrons had the same energy and pitch angle as the particle emitting the most synchrotron radiation. Hence, one can often characterize a synchrotron measurement with the ``dominant particle'' parameters. While one should be careful not to conclude that all particles have the same parameters from this, determing the dominant particle parameters can greatly help in modelling the scenario appropriately.

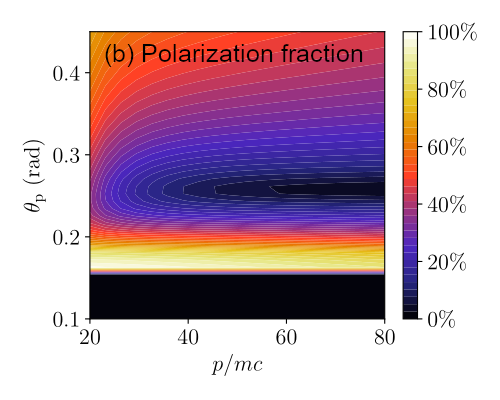
Figure 1 Examples of SOFT simulations for a JET-like ($B_0 = 3.45\,\mathrm{T}$, $R_{\rm maj} = 2.96\,\mathrm{m}$, $a = 1.25\,\mathrm{m}$) circular plasma with a parabolic current profile and on-axis safety factor $q_0 = 1$. The figures show synchrotron (a) polarization fraction and (b) polarization angle measured by a single MSE polarimeter line-of-sight [5] as a function of the runaway electron momentum $p$ and pitch angle $\theta_{\rm p}$.
Polarized synchrotron emission
The light emitted by runaway electrons is linearly polarized, and the polarization degree and direction of this light can be measured using for example MSE polarimeters [4,5]. These polarimeters are usually equipped with a number of narrow lines-of-sight, viewing across the plasma and observing light near the Balmer-$\alpha$ spectral line ($\lambda\approx 656\,\mathrm{nm}$). This is beneficial for observing synchrotron radiation, since the continuous spectrum of synchrotron radiation well covers the polarimeter spectral line, and oftentimes dominates over background radiation.
The direction of the synchrotron radiation polarization vector is determined by the local magnetic field direction as well as the direction of motion of the emitting electron. Most of the radiation is observed to have either vertical or horizontal polarization, with very little light consisting of a clear super-position of the two. Hence, in a fixed magnetic field, a radially varying threshold is found in pitch angle across which the observed polarization sharply transitions between the two directions, as is shown in Figure 1. The sudden transition of the polarization vector also gives rise to a significant drop in the polarization fraction around the threshold. These signatures can help in identifying the pitch angle of the dominant particles, which are key to understanding experimental observations.
References
[1] M. Hoppe et al, Nucl. Fusion 58 026032 (2018).
[2] R. A. Tinguely et al, Plasma Phys. Control. Fusion 60 124001 (2018).
[3] R. A. Tinguely et al, Nucl. Fusion 58 076019 (2018).
[4] R. A. Tinguely et al, Nucl. Fusion 59 096029 (2019).
[5] N. C. Hawkes et al, Rev. Sci. Instrum. 70 894 (1999).
| Affiliation | Department of Physics, Chalmers University of Technology |
|---|---|
| Country or International Organization | Sweden |
