Speaker
Description
ELM control and mitigation efforts are of highest priorities for ITER and beyond. However, often such efforts with RMPs and pellets do not focus on the pedestal turbulence and transport and their effect on ELM characteristics. Detailed analysis of pedestal turbulence as a function of the heating mix may provide crucial insights as well as additional handles for ELM control. It is found that recovery of pedestal pressure gradient in the inter-ELM phase is delayed and magnetic and density fluctuations increase along with excitation of several quasi-coherent modes in the ECH dominated discharges in DIII-D. As a result, ELM frequency decreases by 40% when heating is changed from pure NBI to predominantly ECH. This would be consistent with our hypothesis that turbulence driven transport increases with these quasi-coherent modes and thus keeping the pedestal away from ELM threshold for a longer duration of time, as shown in Fig. 1(a). In this study, localization of these modes at the pedestal is confirmed. Growth of these modes has some correspondence with the steepening of $\nabla T_{e}$ at the pedestal with ECH injection. That these mode activities may lead to enhanced transport at the pedestal steep gradient region in the inter-ELM period is supported by the baseline of the D$_{\alpha}$ signal, which indicates increased particle flux.
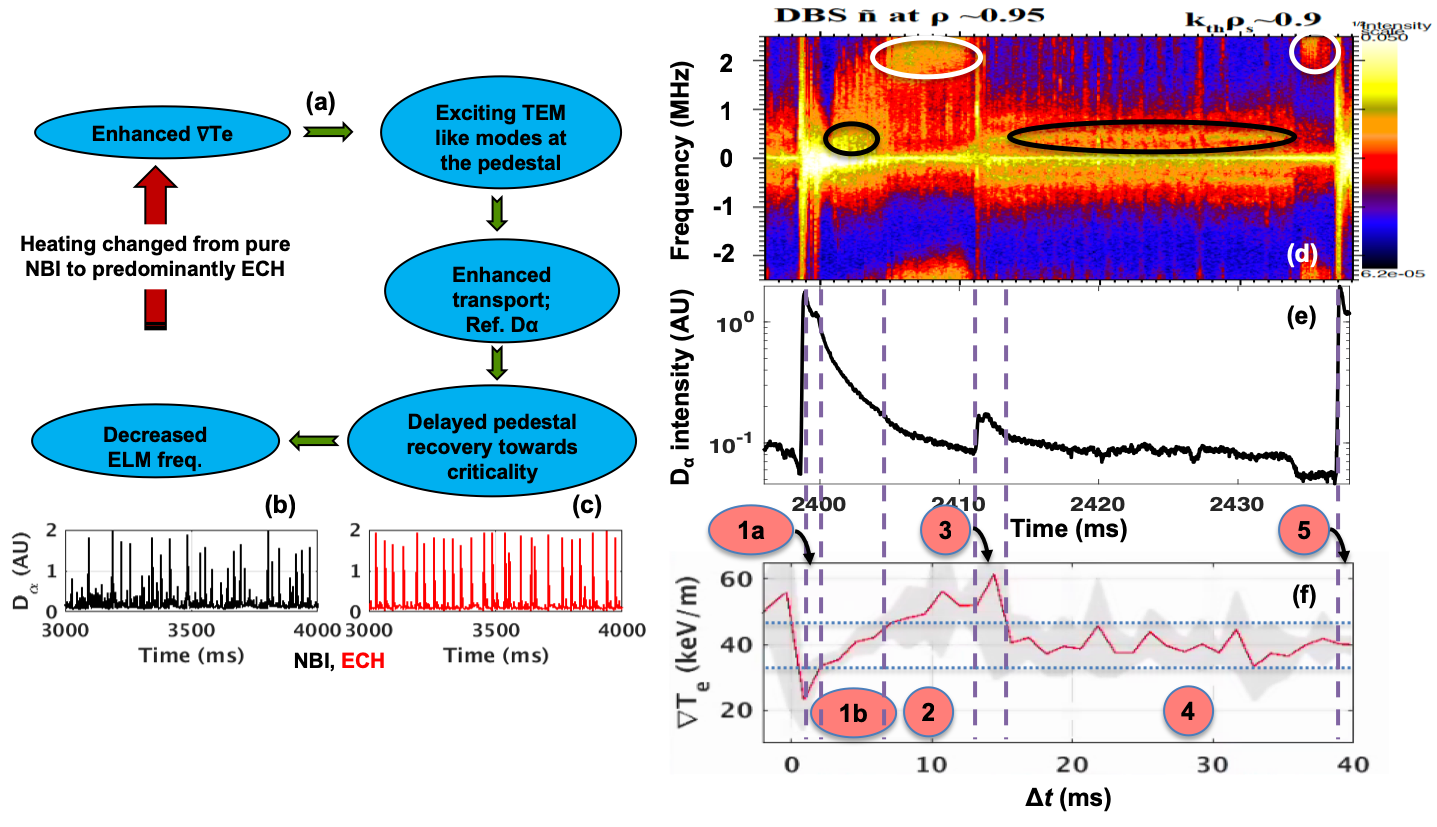
Fig. 1 (right) shows the spectrogram of density fluctuations from a Doppler Backscattering (DBS) diagnostics channel at the steep gradient region ($\rho$ = 0.95) from a candidate ECH shot. It can be seen that there are two modes evolving in the inter-ELM period: following the ELM crash, a low frequency (400 kHz) quasi-coherent mode (LFQC; black oval) is observed in the $\nabla T_{e}$ phases #1b and #4. It is apparent that the LFQC emerges and survives in a narrow range of values of $\nabla T_{e}$, roughly bounded by the two horizontal broken blue lines on $\nabla T_{e}$. On the other hand, high frequency (~2 MHz) broadband fluctuations (HFB; white oval) dominates in phases #2 and #5 leading towards the small Dα spike and the large type-I ELM respectively. Whenever, the LFQC is present (phases #1b and #4), the D$_{\alpha}$ baseline is enhanced indicating increased particle flux. Based on this evolution of $\nabla T_{e}$ the occurrence of these two modes appears consistent with affecting transport and thereby frequency and amplitude of the ELMs. In phase #2, the gradients have reached the threshold for ELMs to occur, while the pedestal heights, especially $n_{e}$ and hence, $p_{e}$ pedestal heights, are still low and evolving. Hence, one or two small spikes in D$_{\alpha}$ are observed in between two consecutive large type-I ELMs.
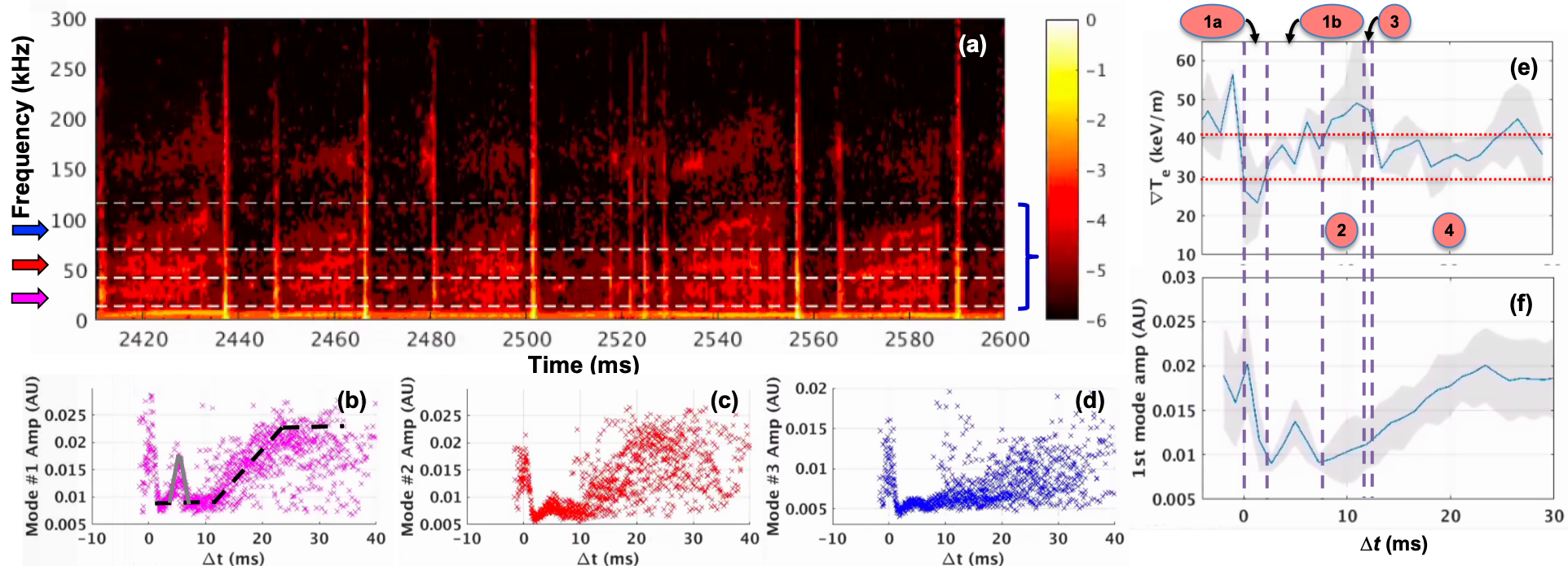
A similar correlation is observed between magnetic fluctuations and $\nabla T_{e}$, as seen in the DBS data. A distinct group of three modes (13~116 kHz) is seen in magnetic fluctuations in Fig. 2. ELM-synced analysis shows that these modes briefly grow and die down in the first 2-7 ms of the inter-ELM period. After that the modes grow again from 13 ms onwards and saturate at ~25 ms. The initial growth bump at ~5 ms and the growth from 13 ms are in $\nabla T_{e}$ phases #1b and #4, similar to the growth patterns of the LFQC in DBS, as shown in Fig. 1.
The heat and particle diffusivities are calculated from the measured profiles in TRANSP. The electron particle diffusivity ($D_{e}$) is much less than the electron heat diffusivity ($\chi_{e}$) in the steep gradient region. As per the recently proposed fingerprint analysis approach [M. Kotschenreuther et al., Nucl. Fusion 59, 096001 (2019)], this suggests that the transport is possibly of the nature of $\nabla T_{e}$ driven, dominated by TEM and MTM. TGLF simulations show that the linear growth rate of the most dominant mode peaks at $k_{\theta}$ρs ~ 0.4 at the steep gradient region. Corresponding frequency is in the electron direction over the entire pedestal for $k_{\theta}$ρs < 1.5, indicating that TEM and/or MTM could be important. This study may provide vital inputs towards understanding inter-ELM pedestal recovery in varied transport regimes and predicting/optimizing pedestal performance and ELM behavior in future reactor grade plasmas. This work is supported by US DOE under DE-SC0019302, DE-FG02-08ER54999, DE-FG02-08ER54984, DE-AC02-09CH11466 and DE-FC02-04ER54698.
| Affiliation | College of William & Mary |
|---|---|
| Country or International Organization | United States |
