MoD-PMI 2025

Time-Dependent Density Functional Theory Analysis of Hydrogen Atom vs. Hydrogen Ion Injection onto a Tungsten Surface

Not scheduled

20m

Press Room (IAEA)

poster

Speaker

Yuto Toda (Graduate Institute for Advanced Studies)

Description

Historically, atomistic simulations of plasma–wall interactions (PWI) have been carried out using methods such as binary collision approximation, molecular dynamics (MD), and density functional theory. In these approaches, an incident particle from the plasma to the wall has been generally substituted by neutral atoms instead of ions due to the limitation of simulation models. However, the extent to which this substitution affects the reproducibility of the simulation is not yet well understood.

One issue that cannot be addressed when an ion is substituted with a neutral particle is the neutralization process in which the incident ion catches electrons on the surface. In the present work, our simulations focus particularly on the ion neutralization process on a tungsten surface.

To simulate the ion neutralization process, we employed Ehrenfest-MD, which is the hybrid method of time-dependent density functional theory (TDDFT) and MD. In this method, the electron dynamics is described by the time-dependent Kohn–Sham (TDKS) equation based on TDDFT, and nuclei motion is described by Newton’s equations of motion. Ehrenfest-MD simulation is performed using the QUMASUN[A. M. I, Y. T, and A. T, Nuclear Materials and Energy 42, 101836 (2025).] code.

We also formulated the ion neutralization probability to interpret the TDDFT simulation results. By approximating the system wave function $\Psi(r_1, \cdots r_n)$ with a Slater determinant constructed from the TDKS orbitals, we can calculate the probability that there are $m$ electrons within any chosen small region $V$:
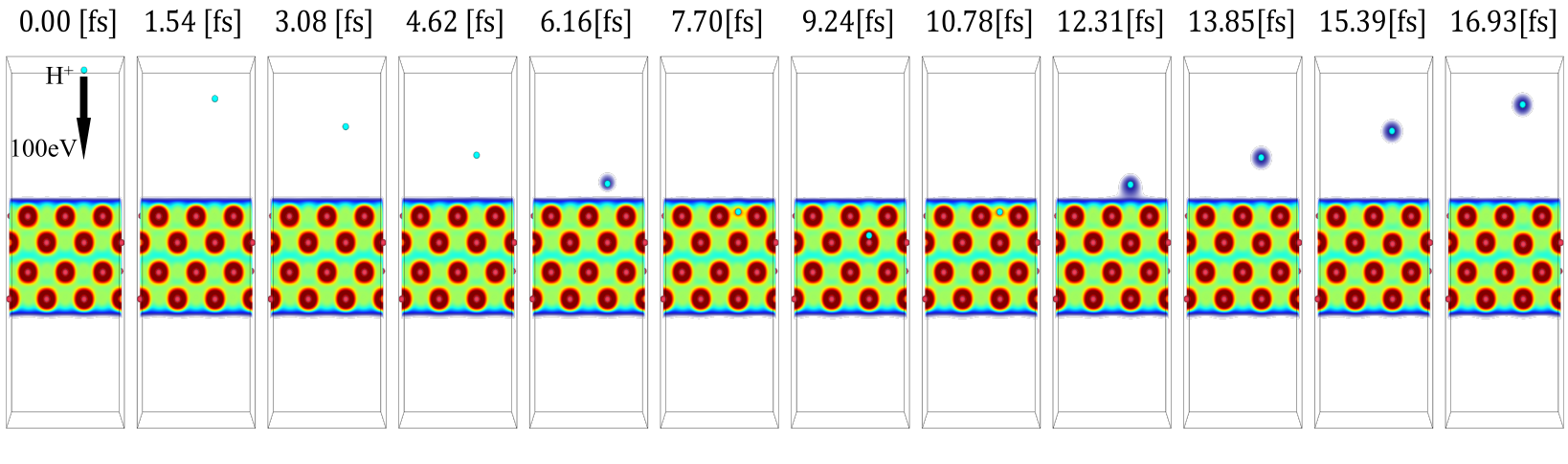
$$ \begin{align} P(m) = & \binom{n}{m} \prod_{i=1}^{m}\int_{ V}d{r_i} \prod_{j=m+1}^{n}\int_{\bar{V}} d{r_j} |\Psi(r_1, \cdots, r_n)|^2. \end{align} $$ Here,$\bar{V}$ is all the regions in the system except the region $V$. As an example, consider a hydrogen ion that has been injected onto a wall, reflected, and then analyzed after it has left the surface sufficiently. If there are no electrons around the hydrogen nucleus, we interpret the hydrogen as being in an ionic state. If there is one electron, we interpret it as neutral, and if there are two electrons, as a negatively charged state. Accordingly, we interpret the probabilities $P(0)$, $P(1)$, and $P(2)$ of finding 0, 1, or 2 electrons around the nucleus as the probabilities of positive ionization, neutralization, and negative ionization, respectively. At the beginning of the simulation, there are no electrons around the hydrogen nucleus, but after reflection from the tungsten surface, the presence of electrons around the hydrogen nucleus is confirmed. In this presentation, we will introduce simulations of the injection of hydrogen ions and hydrogen atoms onto a tungsten (110) surface. Figure 1 shows the snapshots of the simulation of hydrogen ion incidence. At the beginning of the simulation, there are no electrons around the hydrogen nucleus, but after reflection from the tungsten surface, the presence of electrons around the hydrogen nucleus is confirmed. In the hydrogen ion injection, approximately 25% of the hydrogen remains positively ionized, about 50% becomes neutralized, and around 25% becomes negatively ionized at the end of the simulation $t = 16.93$ fs.

Figure 1. Snapshots of hydrogen ion incidence onto tungsten (110) surface. The Hydrogen ion is injected perpendiculary to the surface at 100eV.