Speaker
Description
Non-axisymmetric magnetic field ($B$) configuration is present in linear fusion devices,particularly, those contain minimum-$B$ magnetic field configuration as MHD stabilizer [1,2]. Non-axisymmetric $B$ configuration is also present in toroidal fusion devices, such as, in helical devices [3]. Localized components of non-axisymmetric magnetic field can introduce radial transport of plasma particles [4,5]. This radial loss of plasma can limit the increment of plasma density of the devices [6]. In addition, this transport process may lead plasma wall interaction which may introduce many limitations in the experiment such as, high $\beta$ plasma formation, thermal/barrier potential formation, etc [7,8].
To understand the effect of the localized non-axisymmetric B component, relevant kinetic properties of plasma particles are analyzed numerically. Numerical analysis is done where,$|\bar{B}|=1.3 \text{ T}$, $|\bar{R_c}|=0.5 \text{ m}$, $T_e=50 \text{ eV}$, $T_{||i}=200 \text{ eV}$, $T_{\perp i}=500 \text{ eV}$ and $S=1 \text{ m}$ [9]. The symbols $R_c$, $T_e$, $T_{||i}$, $T_{\perp i}$ and $S$ are the radius of curvature of the magnetic field lines, electron temperature, parallel and perpendicular ion temperature and length of the non-axisymmetric $B$ region, respectively. In this calculation, it is considered that the density of plasma is $\sim10^{14}$ particle/m$^3$. Perpendicular shift of ion and electron due to the combined effect of $\nabla B$ and curvature drifts are calculated using the following equations:
$\begin{equation}
(d_{\perp i})_{drift}=+1.44\times10^{-4}\frac{S\sqrt{T_{\perp i}}}{BR_c} \text{ m; } T_{\perp i} \text{ in eV,} \tag{1a}
\end{equation}
$
$
\begin{equation}
(d_{\perp e})_{drift}=-3.37\times10^{-6}\frac{S\sqrt{T_{\perp e}}}{BR_c} \text{ m; } T_{\perp i} \text{ in eV.} \tag{1b}
\end{equation}$
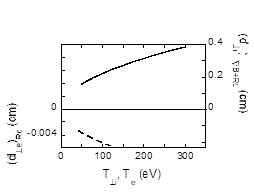
Fig. 1. Dependence of perpendicular shift of the particles - due to the effect of $\nabla B$ and curvature drifts - on temperature.
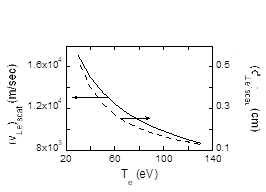
Fig. 2. Perpendicular velocity and perpendicular shift of electron due to small angle Coulomb scattering during passing many ions.
It is found that the ion shifts $(d_{\perp i})_{drift}=0.4 \text{ cm}$ and electron shifts $(d_{\perp e})_{drift}=0.005 \text{ cm}$, i.e. ions shift 80 times more compared to electrons in perpendicular direction (Fig. 1). Electron perpendicular velocity due to small angle Coulomb scattering by ion and the perpendicular shift of electron are calculated using the following equations, respectively:
$\begin{equation}
(v_{\perp e})_{scat}=\langle (\Delta v_{\perp e})_{scat}\rangle = \sqrt{2v_{th-e}\langle(\Delta v_{||e})_{scat} \rangle}; \tag{2a}
\end{equation}
$
$
\begin{equation}
(d_{\perp e})_{scat}= S\sqrt{2\langle(\Delta v_{||e})_{scat} \rangle/v_{th-e}} . \tag{2b}
\end{equation}$
Here, the symbols $v_{th-e}$, $v_{||e}$, and $v_{\perp e}$ are the electron thermal velocity, parallel and perpendicular electron velocity, respectively. It is found that the perpendicular velocity of electron and thereby its perpendicular shift decreases with $T_e$ (Fig.2).
It is found that the perpendicular shift of electrons due to Coulomb scattering is comparable to the perpendicular shift of ion due to the combined effect of $\nabla B$ and curvature drifts. The numerical analysis indicates that the ion drift due to the non-axisymmetric magnetic field and electron displacement due to small angle Coulomb scattering during passing through drifted ions are the candidates of the possible plasma shift in the non-axisymmetric $B$ region [9].
References
1 GOTT, YU.V., et al., Nucl. Fusion Suppl., part 3, 1045 (1962).
2 INUTAKE, M., et al., Phys. Rev. Lett. 55, 159 (1985).
[3] MOTOJIMA, O., et al., Fusion Eng. Des. 20, 3 (1993).
[4] ISLAM, M.K., et al., J. Phy. Soc. Japan, 69, 2493 (2000).
[5] ISLAM, M.K., NAKASHIMA, Y., in “New developments in Nucl. Fusion Res.”, p.1-43; Ed.: Y. Nakamura, Nova Sci. Pubs. Inc., USA; (2006); J. Magnetohydrodynamics,Plasma & Space Res., 12, 161 (2007).
[6] YATSU, K., et al., Chinese Physics Letter 362, 69 (1998).
[7] ISLAM, M.K., et al., J. Applied Physics 100, 033304 (2006)
[8] ISLAM, M.K., et al., Transactions of Fusion Sci. and Tech., 51(2T), 316 (2007)
[9] ISLAM, M.K., et al., J. Phy. Soc. Japan, 69, 2493 (2000).
