Speaker
Description
Nonlinear two-fluid MHD simulations reveal the role of resonant field penetration in ELM suppression and density pump-out in low-collisionality ITER-Similar-Shape (ISS) plasmas in the DIII-D tokamak$^1$. The operational window for ELM suppression in DIII-D ISS plasmas coincides with calculations for magnetic island formation at the pedestal top ($n_e<3\times10^{19}m^{-3}, B_r/B_t >10^{-4}, \nu_e^*<0.3$) based on nonlinear MHD simulations using the TM1 code$^2$. Key phenomenology in experiment are reproduced in the simulations including density pump-out for field penetration at the foot of the pedestal and pedestal pressure and width reduction due to magnetic island formation at the top of the pedestal. TM1 simulations also reproduce the observed $q_{95}$ width of ELM suppression windows in DIII-D. Analysis indicates that wide $q_{95}$ windows of ELM suppression may be accessible in DIII-D and ITER by operating at higher toroidal mode number.
For our analysis we use the cylindrical initial value nonlinear two-fluid MHD code TM1$^2$ with the helical magnetic field boundary condition provided by the ideal MHD code IPEC$^3$. The fully toroidal ideal MHD code IPEC calculates the perturbed 3D magnetic equilibrium (vacuum field plus ideal MHD kink/peeling response to the I-coils) in the actual magnetic geometry. TM1 takes the measured kinetic profiles from DIII-D before the RMP is applied, including initial transport coefficients and neoclassical resistivity from TRANSP. Multiple helical field harmonics from IPEC are applied at the simulation boundary for a given toroidal mode number (e.g. $m/n=6/2, 7/2, 8/2, 9/2, 10/2, 11/2, 12/2$ harmonics for $n=2$ RMP). The TM1 simulation then predicts the penetration or screening of these resonant fields in the plasma interior and the effect of these fields on the electron density and temperature profile. The TM1 model solves the torque balance that governs the bifurcation from screening to penetration of resonant fields including diamagnetic drifts that are important in the pedestal. TM1 also solves the electron continuity and energy transport equations, taking into account enhanced collisional (parallel) transport across magnetic islands.

TM1 simulations show that RMPs readily penetrate into the collisional foot of the DIII-D pedestal near the separatrix ($\psi_N>0.98$), generating a narrow region of edge stochasticity and enhanced collisional transport. The enhanced transport leads to density pump-out, reproducing the magnitude of the observed density reduction observed in experiment$^{1,4}$. While pump-out is ubiquitous at low collisionality, special conditions are required for ELM suppression in DIII-D ISS plasmas, including low plasma density ($<3\times10^{19}m^{-3}$), high co-$I_p$ toroidal rotation and high RMP amplitude ($B_r/B_t >10^{-4}$)$^5$. These conditions correspond to the requirements for resonant field penetration at the top of the pedestal from TM1 simulations. Figure 1 (a) shows the similarity in the TM1 predicted (white) and measured electron pressure profile (yellow) during pumpout and ELM suppression using $n=2$ RMPs in a DIII-D ISS plasma with $q_{95}\approx4.1$, together with the Poincaré plot showing penetration of resonant fields at the top and foot of the pedestal. ELMs are suppressed when the pedestal height and width fall $\approx15\%$ below the EPED model prediction$^6$. Several hundred non-linear TM1 simulations were performed to derive the following scaling relation for the field penetration threshold at the pedestal top in DIII-D ISS plasmas
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ B_{r,th}^{scale}/B_t=3.5\times10^{-2}n_e^{0.7}|\omega_E+\omega_{*e}|^{0.9}B_t^{-1}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $(1)
where $\omega_E$ and $\omega_{*e}$ are the $E\times B$ and electron diamagnetic drift frequency. This scaling closely resembles analytic estimates for error field penetration in the plasma core$^7$ and is quantitatively consistent with the threshold for ELM suppression in DIII-D. A 2D contour plot of the penetration threshold $B_r/B_t$ at the pedestal top versus density and $\omega_E$ is shown in Figure 1 (b). The RMP amplitude for penetration decreases (yellow to blue) as the density and the magnitude of $\omega_E$ decrease, consistent with experiment for ELM suppression$^5$. A database of $n=2$ RMP discharges are overlaid onto Figure 1 (b), with ELM suppression (yellow stars) and ELMing (black stars). The boundary contour between suppression and ELMing corresponds to the maximum available RMP amplitude $B_r/B_t\sim3.5\times10^{-4}$ in the experiment (white dashed line), representing a remarkable level of agreement between experiment and nonlinear MHD theory for the ELM suppression threshold. Analysis of a model ITER $Q=10$ discharge$^8$ predicts that the threshold for $n=3$ penetration at the top of the pedestal will be significantly lower ($B_r/B_t\sim2\times10^{-5}$) than in DIII-D due to the lower rotation and diamagnetic frequency expected in ITER.
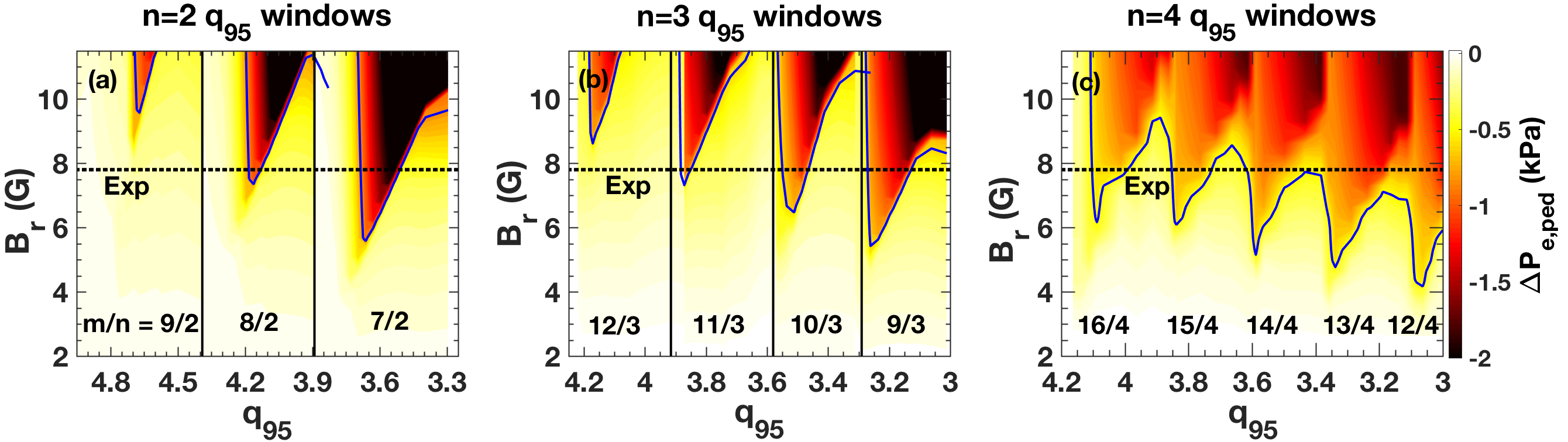
TM1 simulations also reveal the conditions required for wide $q_{95}$ windows of ELM suppression. Wide $q_{95}$ windows are essential for operational flexibility in ITER. However, near the threshold of resonant field penetration at the top of the pedestal, only narrow $q_{95}$ windows of ELM suppression are observed in DIII-D. These narrow windows are reproduced using TM1 simulations and EPED model predictions. Figure 2 shows the predicted pedestal pressure reduction (color contour) versus $q_{95}$ from TM1 simulation and its intersection with the $n=2$ and $n=3$ RMP amplitude on the plasma boundary obtained from IPEC (horizontal dashed lines). For similar RMP amplitudes on the plasma boundary, $n=3$ produces wider $q_{95}$ windows of ELM suppression than $n=2$, consistent with DIII-D experiment$^5$. Figure 2 (c) shows a TM1 simulation with $n=4$ RMPs in DIII-D, indicating window overlap for the same ISS plasma condition. The TM1 simulations predict access to wide operational window of ELM suppression with relatively weak pressure reduction at higher-$n$. Analysis of model ITER equilibria also reveals a similar trend with toroidal mode number, suggesting that operating with dominant $n=4$ RMP, accessible to the ITER ELM coil design, may be advantageous for ITER operation.
To conclude, TM1 simulations quantitatively reproduce ELM suppression windows and density pumpout in the DIII-D tokamak. ITER simulations suggest that the threshold for penetration will decrease relative to DIII-D due to the expected lower $E\times B$ and diamagnetic frequency expected in ITER. Our simulations account for the observed width of $q_{95}$ windows of ELM suppression in DIII-D and indicate that $n=4$ RMPs may be effective to produce wide windows of ELM suppression in ITER.
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, using the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Awards DE-AC02-09CH11466 and DE-FC02-04ER54698.
Reference:
1 Q.M. Hu et al., Phys. Plasmas 26, 120702 (2019).
2 Q. Yu and S. Günter, Nucl. Fusion 51, 073030 (2011).
3 J.K. Park and N.C. Logan, Phys. Plasmas 24, 032505 (2017).
4 Q.M. Hu et al., Nucl. Fusion submitted (2019).
5 C. Paz-Soldan et al., Nucl. Fusion 59, 056012 (2019).
6 P.B. Snyder et al., Phys. Plasmas 19, 056115 (2012).
7 R. Fitzpatrick, Phys. Plasmas 5, 3325 (1998).
8 F.M. Poli et al., Nucl. Fusion 58, 016007 (2018).
| Affiliation | Princeton Plasma Physics Laboratory |
|---|---|
| Country or International Organization | United States |
