Speaker
Description
Search for physical models which support increased magnetic reconnection rates has proven to be an important pursuit in both laboratory plasmas such as magnetic fusion plasma devices as well as in astrophysical plasmas. Over the years, it has been realized that apart from ion Hall effect, magnetic field structure and flow field structure near a reconnection zone could be crucial in realizing improved reconnection rates. In this work, a new reduced Hall magnetohydrodynamic model (RHMHD) [7] is used, which captures, apart from the standard reconnection physics, the Hall effect and the effect of plasma flow field, in the out-of-plane and in-plane directions to the reconnection zone. Using magnetic island coalescence as a test problem, we report enhanced reconnection rates.
Sweet-Parker (SP) model is one of the most studied analytical models to explain magnetic reconnection using resistive MHD equations, according to which, the rate of magnetic reconnection $\propto \eta^{1/2}$ ($\eta$ is the electrical resistivity). Hence, for weakly resistive/collisional or collisionless systems, reconnection rate is slow compared to the observed high reconnection rate, within this model. Besides resistive MHD model, studies have been performed using other physics models such as two-fluid Hall MHD model [5], hybrid models [8], fully kinetic models [9], etc, to understand various aspects of magnetic reconnection. These studies have revealed the dependence of reconnection rate on various parameters such as Lundquist number ($\propto \eta^{-1}$), system size, guide field, effect of electron inertia, and more. Presence of a strong external magnetic field helps to study magnetic reconnection using a more simpler model such as Reduced-MHD (RMHD) model [1]. For low resistivity plasmas, kinetic effects such as Hall effect is necessary to incorporate in one-fluid RMHD model. For example, two-potential incompressible Hall MHD model has been used to study self-driven and externally driven magnetic reconnection [11]. Similarly, a more general model is Reduced Hall MHD (RHMHD) model [7]. RHMHD model is described by solenoidal velocity and magnetic field, generated from four scalar potentials. This RHMHD model has been tested in studying effect of Hall physics in turbulence [7], but not much work has been done in the study of magnetic reconnection.
In 2.5-Dimension, when the Hall parameter (ratio of ion skin depth to the characteristic length of the system) and perpendicular potential components initialize to zero, the RHMHD model reduces to Reduced MHD model [1]. In 3D, even for extremely small values of Hall parameter and zero perpendicular potential components, this model retains the helical nature of magnetic and velocity fields. These helical magnetic and velocity components make the 3D flux tubes more realistic as found in tokamak and solar corona. Hence, this RHMHD model is perhaps more suitable to investigate reconnection physics.
One of the important issues is to investigate the role of Hall physics including the flow dynamics along and across the guided $B$-field as flow critically controls the plasma dynamics around reconnection zone. As a test case, magnetic island coalescence problem [3,4,6] has been studied to understand the physics of magnetic reconnection. So, in this work, we investigate the island coalescence problem using the ``Reduced Hall MHD (RHMHD)" model [7] in the incompressible limit using a vorticity-vector potential model within a single fluid framework. As is well known, using Fadeev's equilibrium [2], in the current island coalescence instability, magnetic reconnection is driven by the attraction force between two nearby parallel currents islands. The current sheet thus formed between the islands, because of this attraction force, acts as a reconnection site. In resistive MHD model, for smaller resistivity values, the flux pile-up in currents sheet inhibits further attraction between the current isl7] is used, which captures, apart of the standard reconnection physics, the Hall effect and the effect of the plasma flow field, in the out-of-plane and in-plane directions to the reconnection zone. Using magnetic island coalescence as a test problem, we report enhanced reconnection rates.
To investigate some of these issues, a 2D/3D Reduced MHD solver has been developed. Using this solver, we address the evolution of Fadeev's equilibrium [2] when perturbed. We numerically calculate the eigenfunctions (SEE Fig.1 and Fig.2) and have compared our results with those given in Ref. [4]. In Figure.3, growth rate of island coalescence instability for different island sizes has been plotted (from our code and from Ref.4). To further benchmark our code in the limit of zero Hall parameter, we have plotted time variation of the position of O-point (see Fig.5) and compared our results with those of Ref.[5].
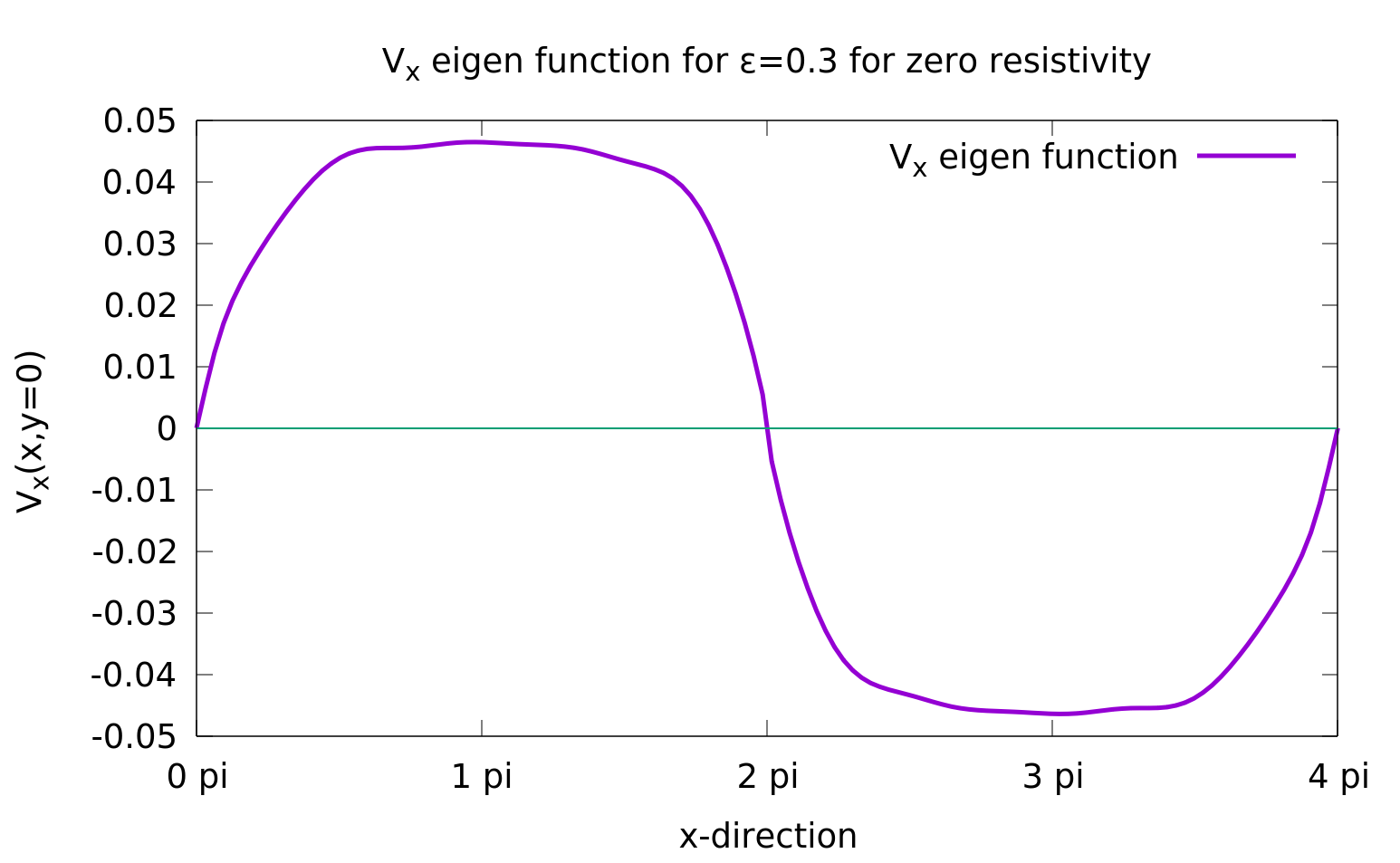
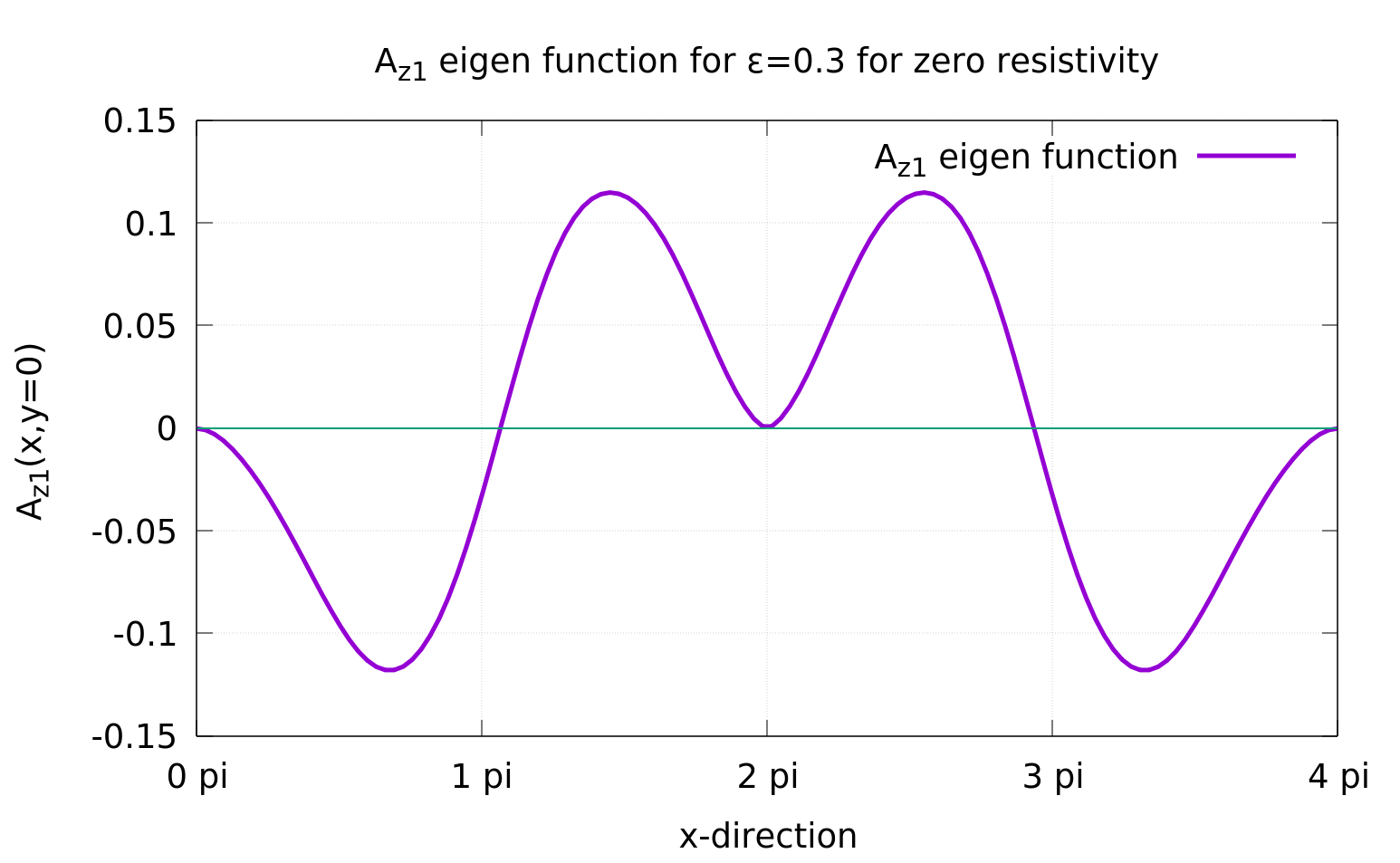
![Growth rate variation with island size for Fadeev's equilibrium (Ref.[4])](http://www.ipr.res.in/fec2020/images/Fig3_FEC2020_JM.png)
![O-point position of islands with resistivity (Ref.[5])](http://www.ipr.res.in/fec2020/images/Fig4_FEC2020_JM.png)
With this model and a well-tested code, we study current island systems for various values of above-stated parameters such as finite resistivity, finite non-zero Hall parameter, different magnetic island sizes, etc. The effect of perpendicular component of vector potential and stream function in RHMHD model [7] is found to change the dynamics of island evolution. This, in turn, controls the evolution as well as reconnection rate of flux tubes in 3D. A detailed study of these 2.5D island structures and 3D flux tubes will be presented.
References:
[1] H. R. Strauss, Phys. Fluids 19, 134(1976).
[2] V. M. Fadeev et al., Nucl. Fusion 5, 202(1965).
[3] D. A. Knoll, L. Chacon, Phys. Plasmas 13, 032307 (2006).
[4] P. L. Pritchett et. al., Phys. Fluids 22, 2140 (1979).
[5] D. A. Knoll, L. Chacon, Phys. Rev. Lett 96, 135001 (2006).
[6] D. Biskamp, Phys. Rev. Lett 44, 1069 (1980).
[7] D. O. Gomez et. al., Phys. Plasmas 15, 102303 (2008).
[8] K. D. Makwana et. al., Phys. Plasmas 25, 082904 (2018).
[9] W. Daughton et. al., Phys. Rev. Lett. 103, 065004 (2009).
[10] A. Stainer et. al., Phys. Plasmas 24, 022124 (2017).
[11] L. F. Morales et. al., J. Geophy. Res. 110, A04204 (2005).
| Affiliation | Institute for Plasma Research |
|---|---|
| Country or International Organization | India |
