Speaker
Description
In fusion tokamaks, high centrally peaked temperatures and plasma currents increase the fusion reactivity, but can also depress the central magnetic safety factor $q$ down to unity or below, destabilizing periodic sawtooth crashes driven by $m=n=1$ MHD instabilities that flatten the temperature and current density over a radius larger than $q=1$. At sufficiently low axis values $q_o <1$, the 1/1 internal kink with magnetic reconnection is unstable, but for $q_o$ near unity at low magnetic shear $(1/q)(dq/dr)\ll 1$, the strongest instabilities are nearly ideal quasi-interchange (QI) modes that are dominated by flows across the magnetic field [1,2].
Numerical simulation of a DIII discharge shows that QI modes can drive a complete MHD sawtooth crash that flattens the central temperature and current density. It reproduces the characteristic QI crash properties and the differences with the internal kink that match detailed experimental observations [1,2]. The results also support a magnetic well stability criterion [2] in terms of flux surface shaping, beta, and $q$, which explains why early theory and simulations predicted QI mode saturation short of a complete crash and why many $q\simeq 1$ QI-like modes that have been observed in KSTAR [3] and other plasmas require extra local heating or current drive. Additional properties could become important in fusion burning plasmas that operate at pressure gradients and heating levels beyond the reach of present-day experiments.
DIII-D discharge 166564 was used [4] to study the stabilization of the 2/1 neoclassical tearing mode by applying a rotating non-axisymmetric n=1 resonant magnetic perturbation (RMP) field. It was an ITER baseline plasma with $q_o=0.945$, $q_{95}=4.2$, and $q=1$ and 3/2 radii $\rho_1=0.3$ and $\rho_{3/2}=0.6$, in a monotonic q-profile. It had $B_T=1.7$ T, $I_p=0.985$ kA and 10 MW of neutral beam heating, with $\beta_N=2.3$, $\beta_o=7.2\%$, $T_{eo}=2.8$ keV, $T_{io}=3.7$ keV, and $n_{eo}=4.5\times 10^{20}\mathrm{m}^{-3}$ with a nearly flat profile. The Alfv\’en time was $\tau_A=0.46\;\mu$s. Nonlinear MHD simulation of the axisymmetric equilibrium without the rotating RMP field, using the extended MHD code M3D, kept toroidal harmonics $n=0$−7 with normalized kinematic viscosity $\mu=D_n=\chi_\perp=10^{-5}$ and effective parallel thermal conductivity $\chi_\|=7R_o v_A$. The plasma boundary was set at $\rho=0.975$ inside the plasma separatrix to reduce the steep density edge gradient.
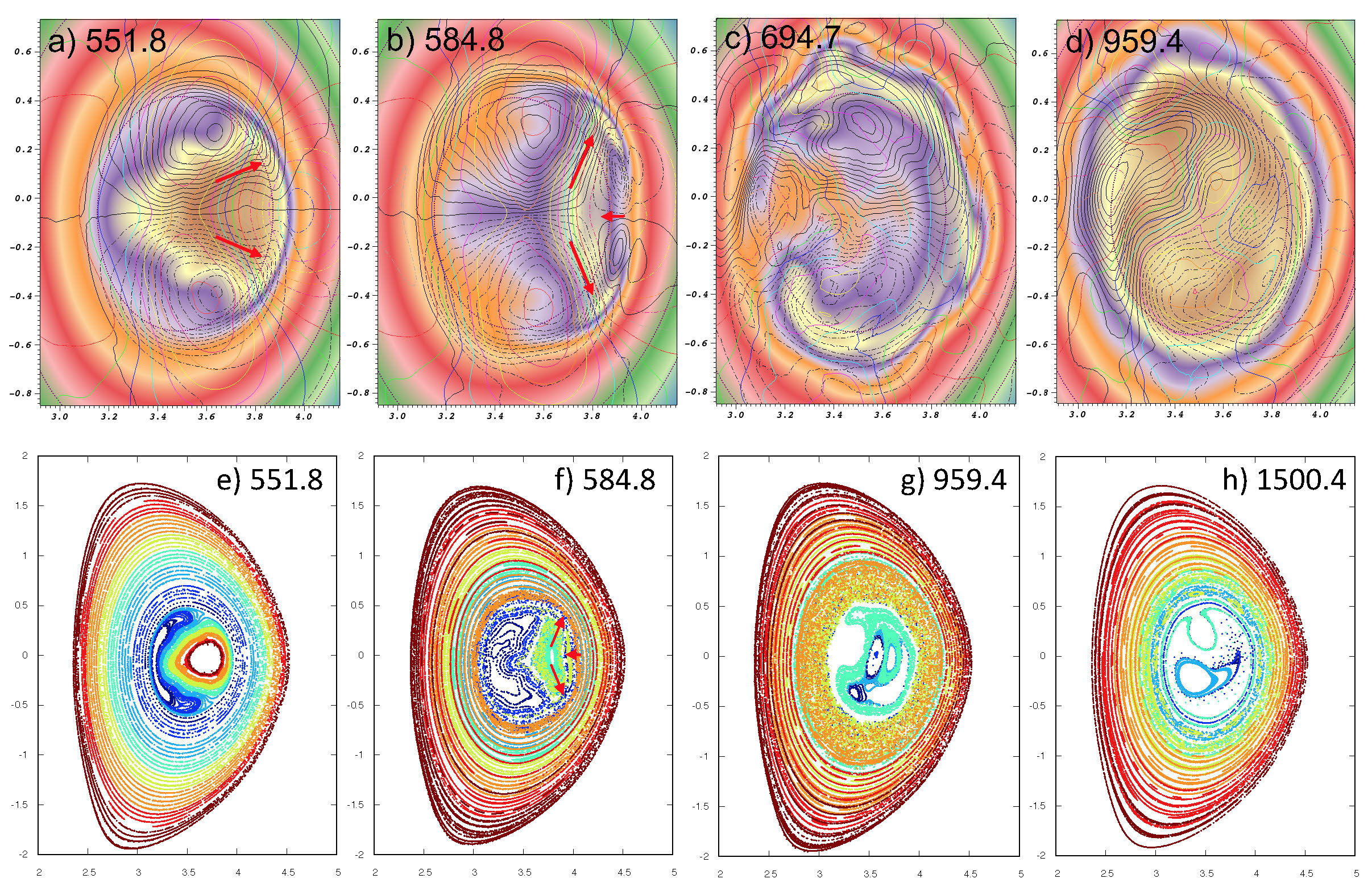
The unstable $q=1$ QI instability found in the simulation is the first example of a truly nonlinear mode with multiple coherently coupled toroidal mode numbers in an axisymmetric plasma. At low amplitude, toroidal harmonics $n=1$ and 2 had nearly equal magnitude. Higher-$n$ harmonics were smaller. Inside $q=1$, the poloidal harmonics were predominantly $m=n$. The individual $n=1$−3 harmonics resembled the corresponding unstable linear perturbations, but were oriented poloidally to maximize the radial outflow (radial displacement) of the 1/1 mode inside $q\le 1$. The multi-mode grew coherently to finite amplitude, when the $n=1$ harmonic began to grow faster and eventually dominated the crash. No strong current layers associated with resonant reconnection appeared at any stage and Lundquist numbers $S=10^6$, $10^7$, and $10^8$ showed similar, nearly ideal MHD evolution.
The large $n=2$ harmonic (2/2 inside $q=1$) had important effects on the early crash. A pair of cool islands grew inward at $q=1$ over the rear half of the 1/1 mode (Fig. 1e,f). They grew widest at the location of the strongest inflow of the total $n=1$ and 2 convective cells, contributing to the apparent $n=1$ kink displacement of the peak temperature from the magnetic axis (Fig. 1a,b). The hot plasma was pushed outward against the forward $q=1$ surface, where it spread poloidally as a consequence of the low shear QI suppression of magnetic reconnection at $q=1$. Although the temperature appears to follow the magnetic surfaces, the magnetic perturbations are weak and the QI flows are the primary driving force. The outflow of the two large $m\simeq 1$ convective cells, originally directed radially outward along the 1/1 mode axis (to the right on the horizontal midplane in Fig. 1) diverged poloidally to more than 60 degrees on either side (Fig. 1a,b). The small reversed flow cells between them helped to narrow the hot region and align the pressure along the strong flow, until strong interchange flows carried the hot plasma out well beyond $q=1$ in a sudden fast crash (Fig. 1b,f, resulting in 1c,g). The central $q$ rose to unity.
The central current density $J_\phi$ flattens over the same radius $r\lt r_{mix}$ as $T$, but over a much longer time, at $t=1500\tau_A$ compared to $959\tau_A$ for $T$. A similar delay was observed experimentally [2]. It differs from the internal kink crash, where both $T$ and $J_\phi$ flatten simultaneously after the final loss of the hot magnetic core from inside $q=1$. At low magnetic shear, the cross-field QI flows create a small amount of magnetic stochasticity with very small $\delta B/B$ over the regions that they traverse. The final current flattening occurs as the crash-generated magnetic stochasticity inside and outside $q=1$ (Fig. 1g) decays away completely (Fig. 1h).
The low-$n$ nonaxisymmetry of the expelled pressure outside $q=1$ drives a transient higher-$m$ ballooning mode, originally shown for the internal kink by W. Park, that helps disperse it further. It can be partially seen in the outer temperature bulges in Fig. 1c, but has mostly healed by the time the central temperature has flattened.
No sawteeth appear in the actual plasma, where the very slowly rotating RMP penetrated to the axis and appeared to stabilize the mode (to be discussed elsewhere). However, the simulation closely resembles the QI sawteeth observed experimentally in other plasmas, including in DIII-D [2]. Comparison to earlier simulations of the internal kink crash with M3D [5] show that MHD simulations reproduce the major observed QI and internal kink sawtooth differences.
After the central crash and healing, small QI-type flows continue inside $q\le 1$ at the reduced central $T_o$. A quasi-steady QI perturbation develops inside $q=1$, also with $n=1$ and 2 harmonics of comparable magnitude, and supports an off-axis partial annulus of higher $T$ that sits inside a weak magnetic island maintained by flows. This resembles the actual plasma configuration and also the central $q\simeq 1$ region of “hybrid” fusion plasmas. The results suggest that quasi-interchange type instabilities, including nonlinearly generated fast interchange flows, may play a larger role in plasma dynamics than generally appreciated.
Work partially supported by the US Department of Energy under DE-SC0007883, DE-FG02-04ER54761, and the China Scholarship Council (L.Xu). Most simulations were carried out at NERSC under Contract No. DE-AC02-05CH11231.
[1] A.W. Edwards, et al., Phys Rev. Lett. 116, 210 (2016); J. A. Wesson, Plasma Phys. Controlled Fusion 28, 243 (1986).
[2] E. A. Lazarus, et al., Phys. Plasmas 14, 055701 (2007).
[3] G. H. Choe, et al., Nucl. Fusion 55, 013015 (2015).
[4] M. Okabayashi, et al., IAEA FEC (2016) EX-P3/16.
[5] L. E. Sugiyama, Phys. Plasmas 21, 022510 (2014); Nucl. Fusion 55, 073006 (2015).
| Affiliation | Massachusetts Institute of Technology |
|---|---|
| Country or International Organization | United States |
