Speaker
Description
The transport, accumulation and control of the W impurity ions are very important issues for the development of ITER.
This work is an analysis of the heavy ion turbulent transport. A new pinch mechanism is found. This strongly nonlinear process is theoretically validated in the frame of a complex test-particle model. The conditions for which the pinch velocity $V$ is experimentally relevant are determined, and the main parameters that could be used to control $V$ are identified.
The origin of the pinch is a special type of order generated by an average poloidal velocity $V_t$ superposed on the $E\times B$ stochastic drift. It consists of two average radial velocities in opposite directions, which exactly compensate. This pair of drifts found in 2 are named hidden drifts (HDs), because they do not yield an average velocity in these conditions. We show that the perfect symmetry of the HDs is destroyed by the polarization drift and by the parallel acceleration, which drive radial pinches.
The validation of the HDs
The HDs are found using a semi-analytical approach, the decorrelation trajectory method (DTM, 1). They are the consequence of the existence of average displacements conditioned by the initial potential $\varphi^0$, $〈x(t)〉_{\varphi^0}$, which have the sign correlated to the sign of $\varphi^0$.
Direct numerical simulations are performed for the validation of the HDs. The conditional averages $〈x(t)〉_{\varphi^0}$ obtained from the numerical data are shown in Figure 1 as functions of $\varphi^0$. The sign correlation between the displacements and the potential clearly appears, as in the DTM results [2, 3].
The transport model
A complex test-particle model is used for the analysis of impurity transport. It is based on the equation of motion of the ions with mass and charge numbers $A$ and $Z$, which includes the polarization drift and the parallel acceleration, besides the stochastic $E\times B$ velocity and the poloidal average velocity $V_t$. It is also necessary to consider ion collisions, because they can strongly affect the order represented by the HDs. The average poloidal velocity $V_t$ contains plasma rotation, the magnetic drifts and the drift of the potential with the diamagnetic velocity. The spectrum of the stochastic potential corresponds to drift type turbulence and the collisions are represented by a colored noise with the collision frequency $\nu$ dependent on $A$ and $Z$. The main dimensionless parameters of the model are
$K_{*}^{'}=\frac{e\Phi}{T_i}\frac{a}{\rho_i} \,$, $C_A=\frac{A}{Z}\frac{\rho_i}{a} \,$, $P_{acc}=\frac{e\Phi}{T_i}\frac{Z}{\sqrt{A}} \,$, $P_c=\frac{\rho_i\nu}{V_*} \,$, $\frac{\tau_d}{\tau_0} \,$, $\frac{V_t}{V_*}$
where $\Phi$ is the amplitude of the potential, $\rho_i$ is the Larmor radius of plasma ions with thermal velocity $v_{thi}$, $T_i$ is their temperature, $a$ is the small tokamak radius, $V_{*}=\rho_i v_{thi}/{a}$, $\tau_0=a/v_{thi}$, and $\tau_d$ is the decorrelation time. The latter is a complex Lagrangian function determined by the combined effects of the time variation of the potential and of the average parallel and poloidal velocities. $\tau_d$ describes the decorrelation of the trajectories from the potential. $K_{*}^{'}$ is the measure of turbulence amplitude, $C_A$ is the parameter of the polarization drift, $P_{acc}$ represents the parallel acceleration effect and the strength of the collisions is shown by $P_c$.
Radial pinch determined by the polarization drift and by the parallel acceleration
The HDs represent a reservoir of radial pinch, because any perturbation of their exact equilibrium provides an average velocity. We have shown 3 that a radial drift velocity $V_{HD}$ yields as the combined effect of the HDs and of the polarization drift. The effect is strong at values of the parameter $C_A>0.1$, which correspond to present plasma characteristics (relatively small values of $Z$ and of plasma size $a/\rho_i$). The aim of the present study is to examine the effects of the parallel acceleration and of collisions on the pinch velocity.
We have found that the parallel acceleration combined with the HDs represents an additional mechanism for the generation of a radial pinch $V_r$ that appears even for $C_A=0$. Typical results of $V_r$ as function of the decorrelation time are shown in Figure 2. The parameter of the parallel acceleration $P_{acc}$ increases with the increase of $Z$ and is not dependent on plasma size. Consequently, this pinch is expected to be dominant in ITER plasmas.
The characteristics of the radial pinch
An important property of both pinch velocities $V_{HD}$ and $V_r$ is that they are antisymmetric functions of the poloidal average velocity $V_t$. The negative (inward) direction is reversed by the change of the sign of $V_t$. Both velocities are increasing functions of $K_{*}^{'}$ and have complex dependences on $\tau_d$, as seen in Figure 2 for $V_r$.
The acceleration induced pinch $V_r$ increases with $Z$, as seen in Figure 2 by comparing the solid lines (cyan for $Z=20$, blue for $Z=30$ and red for $Z=40$). It also depends on the energy of the impurity ions. A significant increase of the pinch appears as the energy decreases (see the red curves, dotted for $W=1.5$, solid for $W=1$ and dashed for $W=0.5$).
The dependence of the pinch $V_r$ on the poloidal velocity consists of a strong increase with the increase of $V_t$ in the range of small $V_t$ followed by a slower decay. The strong influence of $V_t$ can be seen in Figure 2 by comparing the red solid line with the black line, which differ only in the values of $V_t$. The collisions have a weak effect on $V_r$.
The pinch $V_{HD}$ has a rather complicated dependence on $V_t$ (as seen in Figure 3, black curve). A detailed analysis of its characteristics is presented in 3. We have studied here the effect of collisions, which is strong, as seen in Figure 3 (red dots). However, collisions do not influence the dependence of $V_{HD}$ on the main parameters, but only attenuate the pinch at levels that are still significant for the transport. Synergistic effects between $V_{HD}$ and $V_r$ can appear.
Conclusions
The main finding of this analysis is a new radial pinch mechanism that is based on the HDs, a special type of ordered motion. Two sources of pinch are found: the polarization drift and the parallel acceleration. The first acts in the conditions of the existing plasmas and the second for large and hot ITER plasmas. A complex dependence of the pinch velocity on the parameters (1) was found. It shown that the most efficient control is provided by the poloidal velocity.
Acknowledgements
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014-2018 under grant agreement No 633053 and from the Romanian Government. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
1 Vlad M., Spineanu F., Misguich J. H., Balescu R., Phys. Rev. E 58, 7359 (1998).
2 Vlad M., Spineanu F., Europhysics Letters (EPL) 124, 60002 (2018).
3 Vlad M., Spineanu F., Phys. Plasmas 25, 092304 (2018).

The conditional average displacements as functions of the initial potential for several time moments $t=0.4$, $2$, $4$, $6$, $20$, $40$.

The pinch velocity $V_r$ as function of the decorrelation time $\tau_d$. The red curves are for $Z=40$ and the normalized energy $E=1$ (solid), $1.5$ (dotted) and $0.5$ (dashed). The cyan curve is for $Z=20$, $E=1$; the blue curve for $Z=30$, $E=1$. The poloidal velocity is $V_t=0.1$ in all cases except the black curve for $V_t=0.3$, $Z=40$, $E=1$.
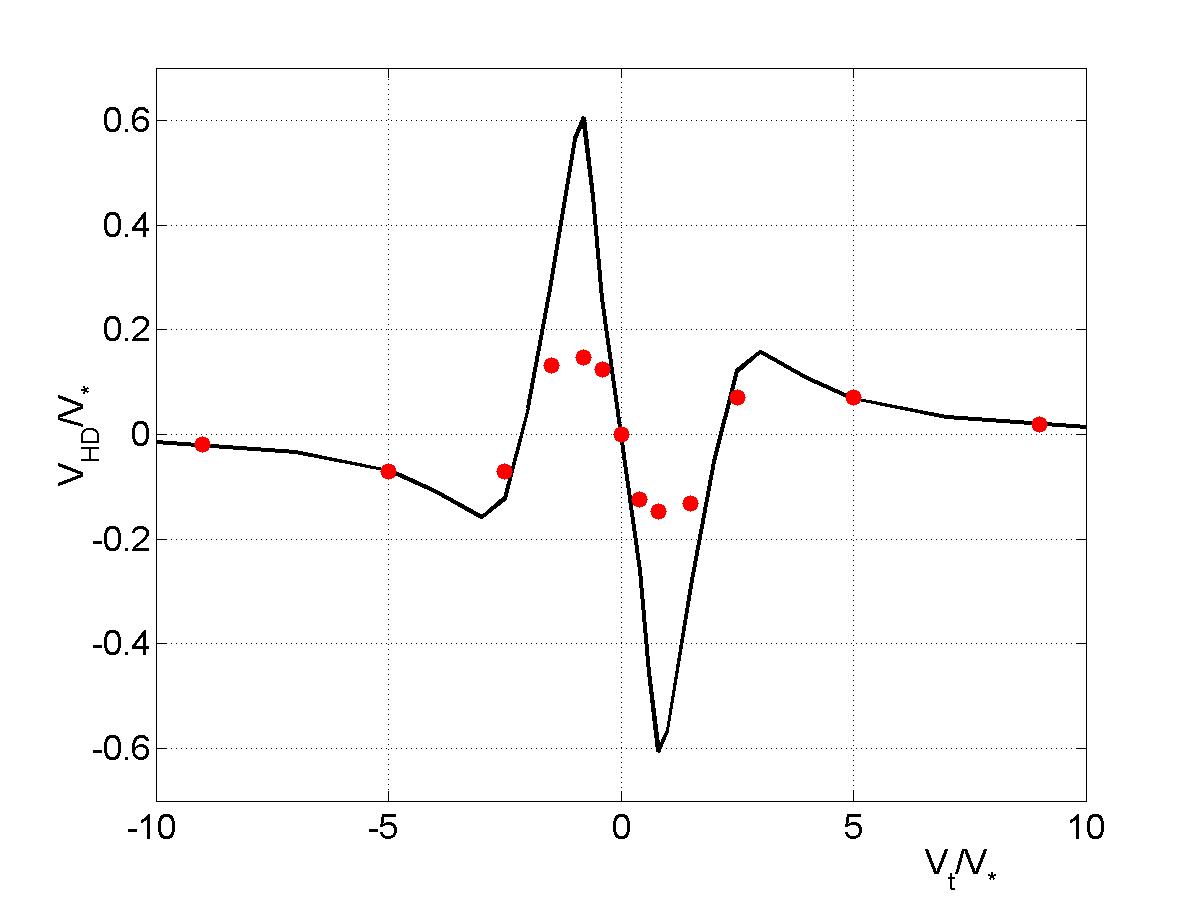
The pinch velocity $V_{HD}$ as function of the poloidal velocity $V_t$ for $K_{*}=10$, $\tau_d=10$, $C_A=0.2$ and for the collision parameter $P_c=0$ (black line) and $P_c=1$ (red dots).
| Affiliation | Nuclear and Radioactive Waste Agency Romania |
|---|---|
| Country or International Organization | Romania |
