Speaker
Description
Power exhaust is considered as one of the most critical issues for future fusion devices. It is considered as an indispensable way for reducing divertor heat load to a tolerable level by seeding impurity and achieving a radiative divertor, especially for the future tokamaks with full metal walls. For China Fusion Engineering Test Reactor (CFETR) [1], which aims to achieve a fusion power ~1 GW, a high total radiation fraction is necessary. However, the impurity seeding is restricted to avoid degradation of the main plasma performance. In this work, the influence of the kind of the seeded impurity species (nitrogen, neon and argon) on the effective plasma ion charge $Z_\rm{eff}$, which is critical for further study on the impurity issues in core plasma and pedestal [2], is emphasized for the high radiative scenario.
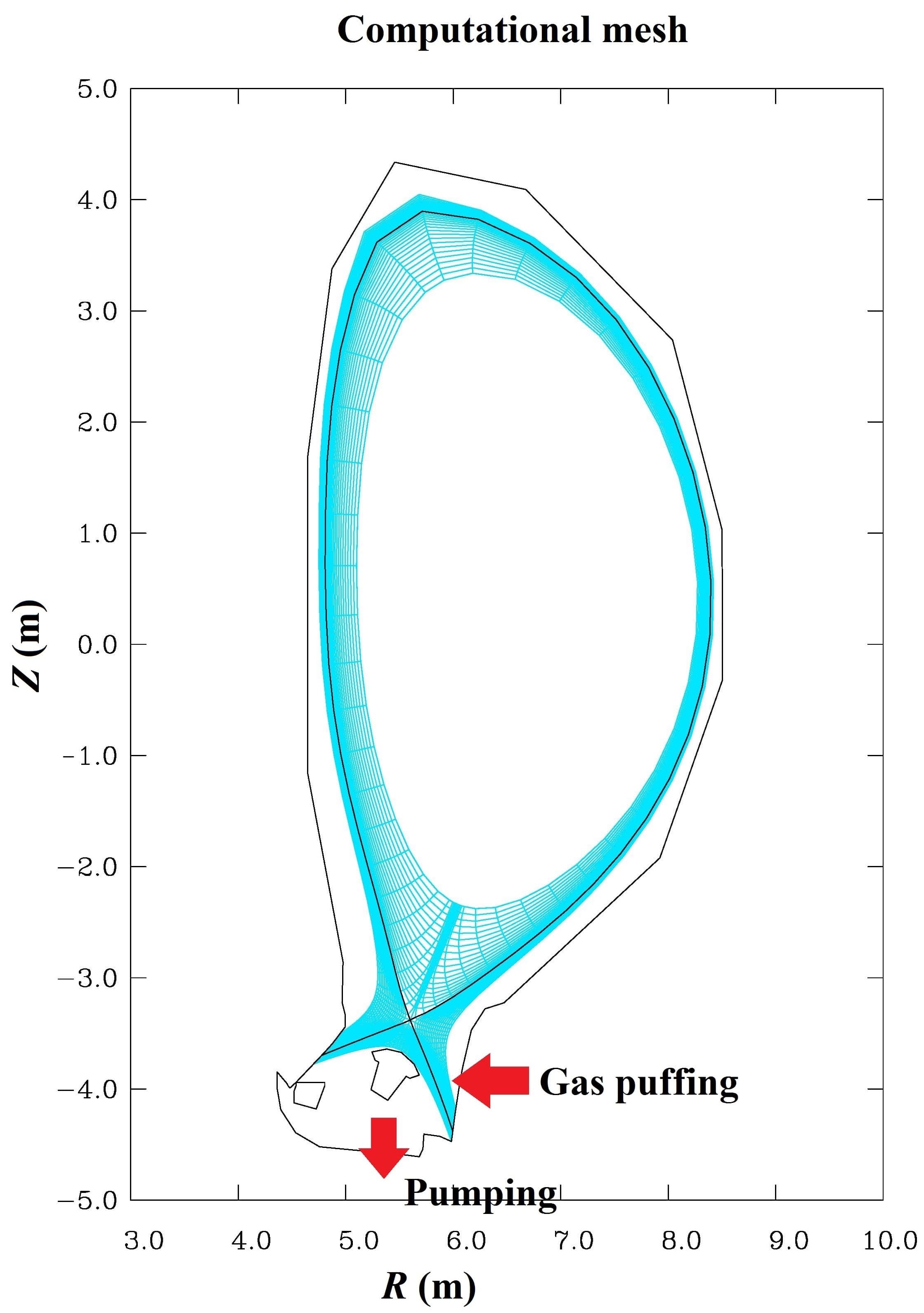
The simulations are performed using SOLPS5.0 code package [3]. Fully tungsten as the first walls and divertor are assumed in simulations. The recycling rates at first walls and divertor targets were fixed to 100% for all species except for the location of pumping. Basic geometry configuration and computational mesh using in SOLPS simulations is shown in Fig. 1, as well as the locations of pumping and gas puffing. The total power across the core-edge boundary is fixed to 200 MW and equally distributes to ions and electrons. A specific set of radially varying cross-field transport coefficients which is identical for all ions account for the pedestal structure predicted by EPED model for CFETR H-mode discharges. A high radiation fraction $f_\rm{rad}$~0.85, which results in detached divertor plasmas is achieved in simulations by injecting a mixture of deuterium gas and different impurity gases. A density scan was performed by varying the deuterium ion density at the core-edge boundary in the range from $6.0 \times {10^{19}}{\rm{\ m}}^{\rm{-3}}$ to $1.0 \times {10^{20}}{\rm{\ m}}^{\rm{-3}}$. The separatrix density is in the range of $2.3{\rm{-}}3.3\times {10^{19}}{\rm{\ m}}^{\rm{-3}}$ and is well below one third of Greenwald density.
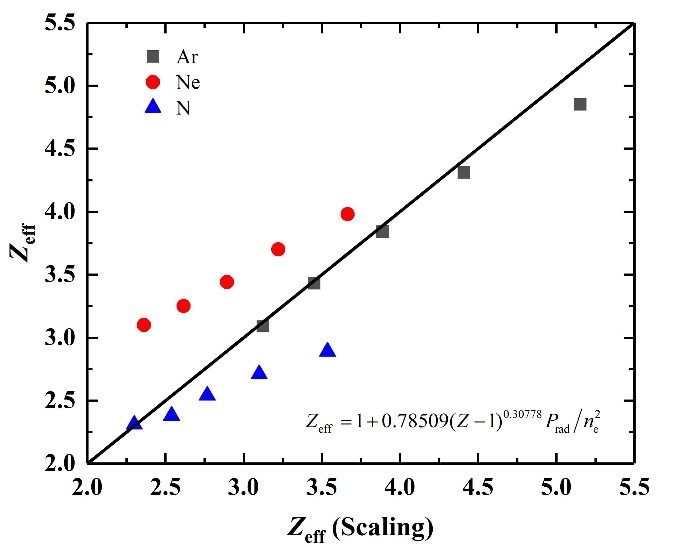
The simulated effective plasma ion charge $Z_\rm{eff}$, electron density $n_\rm{e}$ (both at the core-edge boundary) and the radiated power $P_\rm{rad}$ are fitted according to the Matthews’ scaling [4] from multi-machine database, which results ${Z_{eff}}=1+\left. {0.78509{{(Z-1)}^{0.30778}}{P_\rm{rad}}} \middle/{n_\rm{e}^2} \right.$ as shown in Fig. 2, where different trends can be found for different impurity species. Meanwhile, the fitting formula implies that, the the higher atomic number of the seed impurity $Z$ is, the better performance (i.e. lower $Z_\rm{eff}$ with same $P_\rm{rad}$ and $n_\rm{e}$ ) can be obtained, which is not the result according to the simulation. In order to figure out which impurity species has better performance, the radiative efficiency ${H(Z_\rm{eff})} = \left. {f_\rm{rad}} \middle/{(Z_\rm{eff}-1)} \right.$ is plotted in Fig. 3. For the three chosen impurity species, we have $Z_\rm{Ar} \gt Z_\rm{Ne} \gt Z_\rm{N}$, while for the radiative efficiency $H(Z_\rm{eff})$, it is ${H(Z_\rm{eff},\rm{N})} \gt {H({Z_\rm{eff}},\rm{Ar})} \ge {H(Z_\rm{eff},\rm{Ne})}$.
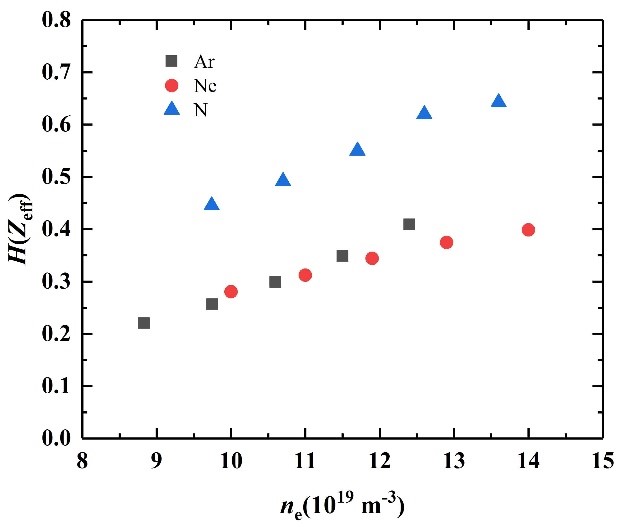
It is noteworthy that there is a relationship of ${E_\rm{ion}^\rm{Ne}} \gt {E_\rm{ion}^\rm{Ar}} \gt {E_\rm{ion}^\rm{N}}$ for the ionization potential $E_\rm{ion}$ of impurities, which follow the same sequences of the radiative efficiency $H(Z_\rm{eff})$. For different impurities, a larger ionization potential leads to ionizations closer to the upstream (according to the ionization source) and longer resident time $\tau$ in the plasma (based on the DIVIMP calculation). When obtaining the Matthews’ scaling, the non-coronal effect is omitted. However, in the SOL region, $\tau$ can be less than 1 ms, which leads to a non-coronal condition. The omitted non-coronal effects may be one of the reasons for the discrepancies with different seeding impurities.
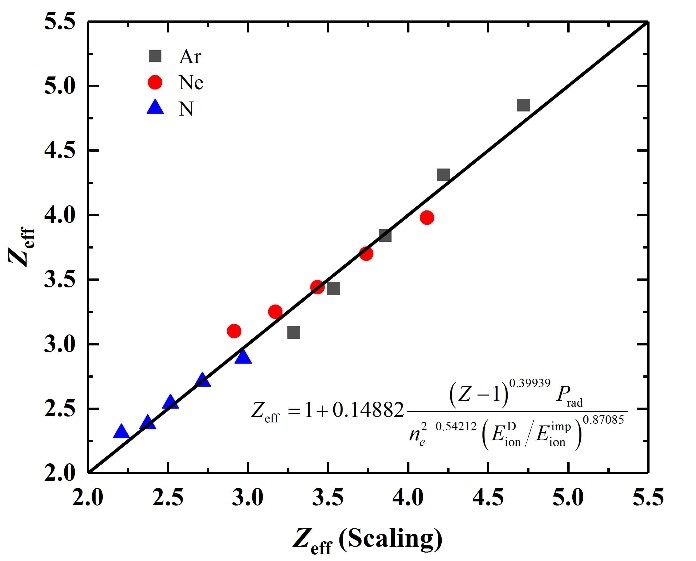
Because it is beyond our ability to give a precise quantitative description of the non-coronal effect in the edge plasma, a simple relationship, i.e. the radiated power coefficient ${L_\rm{non-coronal}} \propto \left. {L_\rm{coronal}} \middle/ {n_\rm{e}^\beta} ({\left. {E_\rm{ion,imp}} \middle/ {E_\rm{ion,D}} \right.})^\gamma \right.$, is assumed. Thus, a modified formula is brought out to include the influence of non-coronal effect, ${Z_{eff}}=1+\left. {0.14882{{(Z-1)}^{0.39939}}{P_\rm{rad}}} \middle/{n_\rm{e}^{2-{0.54212}}} ({\left. {E_\rm{ion,D}} \middle/ {E_{\rm{ion},{imp}}} \right.})^{0.87085} \right.$. It can be seen that, the discrepancy for the trends of different impurity species does not appear. Furthermore, the result shows a dependence of ~$n_{\rm{e}}^{-1.5}$, which is in consistent with the experiment results of JET with high radiation and low core pollution [5].
In summary, we have performed SOLPS simulations for CFETR with different radiation impurity species, i.e., N, Ne and Ar. The radiative efficiency for different impurity species indicates that $H(Z_\rm{eff})$, it is ${H(Z_\rm{eff},\rm{N})} \gt {H({Z_\rm{eff}},\rm{Ar})} \ge {H(Z_\rm{eff},\rm{Ne})}$. It implies that, in case of nitrogen can not be seeded due to the tritium issues, Ar is preferred. Furthermore, a modified formula by introducing the non-coronal effect in the Matthews’ scaling is brought out for fitting the simulated $Z_\rm{eff}$, $n_\rm{e}$ and $P_\rm{rad}$. As a result, the discrepancy for the trends of different impurity species when fitted by Matthews’ formula is improved.
Reference
[1] Y.X. Wan, et al., Nucl. Fusion 57 (2017) 102009.
[2] N. Shi et al, Nucl. Fusion 57 (2017) 126046.
[3] R. Schneider et al., Contrib. Plasma Phys. 46 (2006) 3-191.
[4] G.F. Matthews, et al., J. Nucl. Mater. 241-243 (1997) 450-455.
[5] J. Rapp, et al., J. Nucl. Mater. 390-391 (2009) 238-241.
| Affiliation | University of Science and Technology of China |
|---|---|
| Country or International Organization | China |
